Advanced Topics in Rendering⚓︎

Advanced Light Transport⚓︎

Unbiased Light Transport Methods⚓︎

Bidirectional Path Tracing (BDPT)⚓︎

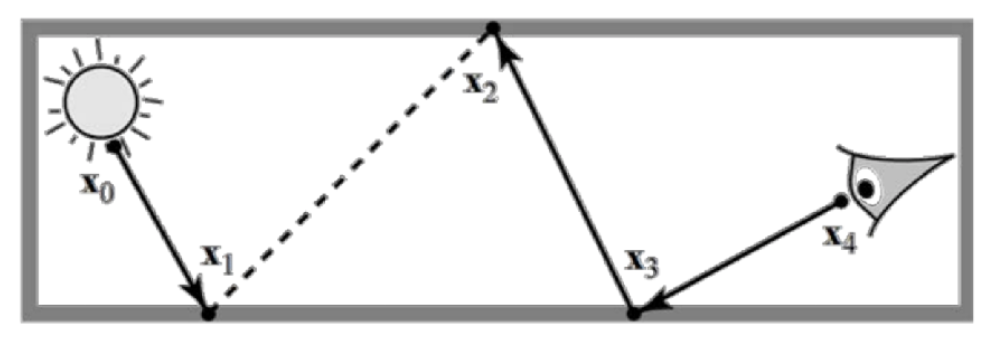
回忆一下，这里的 "path" 是指连接相机和光源的路径。

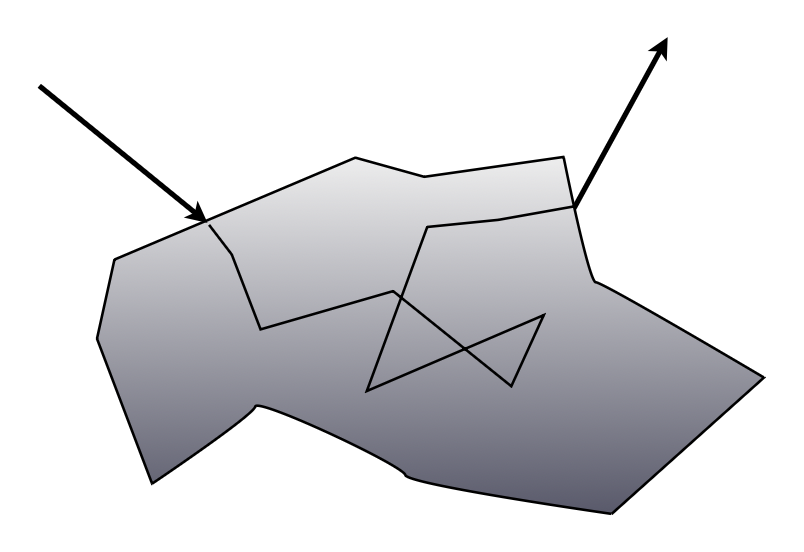
双向路径追踪(bidirectional path tracing) 的思路是：

• 分别追踪来自光源和相机的半路径 (sub-path)
• 然后连接这两条半路径的端点

• 该方法适用于光源侧光线传播情况很复杂的情况
• 但该方法不仅难以实现，而且执行起来很慢

例子

由于这个场景的光源是向上打的，因此整个房间的大多数光来自环境的反射而非光线直照，这就属于“光源侧光线传播情况很复杂的情况”。

Metropolis Light Transport (MLT)⚓︎

Metropolis 光线传播的思路是：

• 马尔可夫链(Markov chain) + 蒙特卡洛：
  • 简单来说，马尔可夫链是统计学中的一种采样工具，它能根据当前样本来生成下一个样本
  • 一个结论是：当被积函数和 PDF（概率密度函数）形状一致时，方差最小，因此利用马尔可夫链，直接沿着 PDF 采样，得到的结果就非常理想了
• 该方法在探索局部但复杂的光线路径时非常有用

• 关键思想：通过局部扰动 (perturb) 一条已有的光线来产生新的光线

  

优点

• 在复杂的光线路径上表现很好
• 是一种无偏方法

缺点

• 难以估计其收敛速率
• 无法保证每个像素有相等的收敛（“局部”处理的坏处）
• 体现在渲染结果上就是看起来“脏脏的”
• 因此该技术通常不会用在渲染动画上
  • 上一帧和下一帧各自有不同的收敛，导致看起来视频抖动非常严重

Biased Light Transport Methods⚓︎

Photon Mapping⚓︎

光子映射(photon mapping) 是一种有偏方法，非常擅长处理镜面 - 漫反射 - 镜面（SDS）路径并生成焦散(caustic) 效果（由于光线聚焦形成的光斑）。

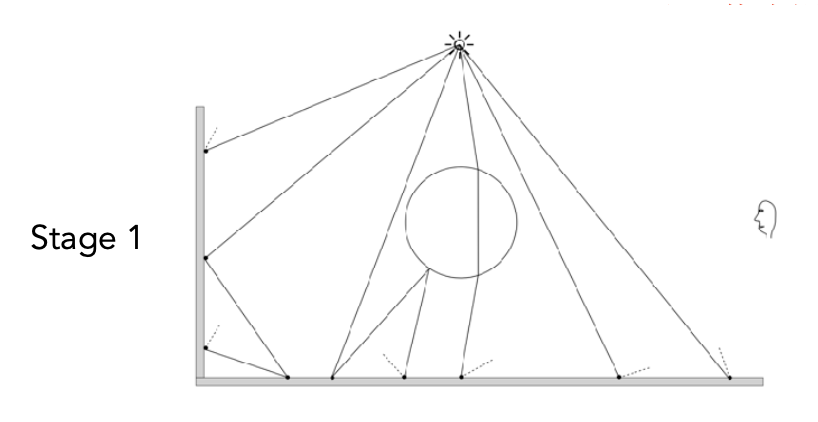
光子映射的实现分为两个阶段：

1. 光子追踪：从光源处发射光子，使其四处弹射，然后在漫反射面上记录光子（也就是说光子最终停留在漫反射面上）

   

2. 光子汇集（最终聚集）：从相机处发射半路径，使其四处弹射，直到打到漫反射面上停止

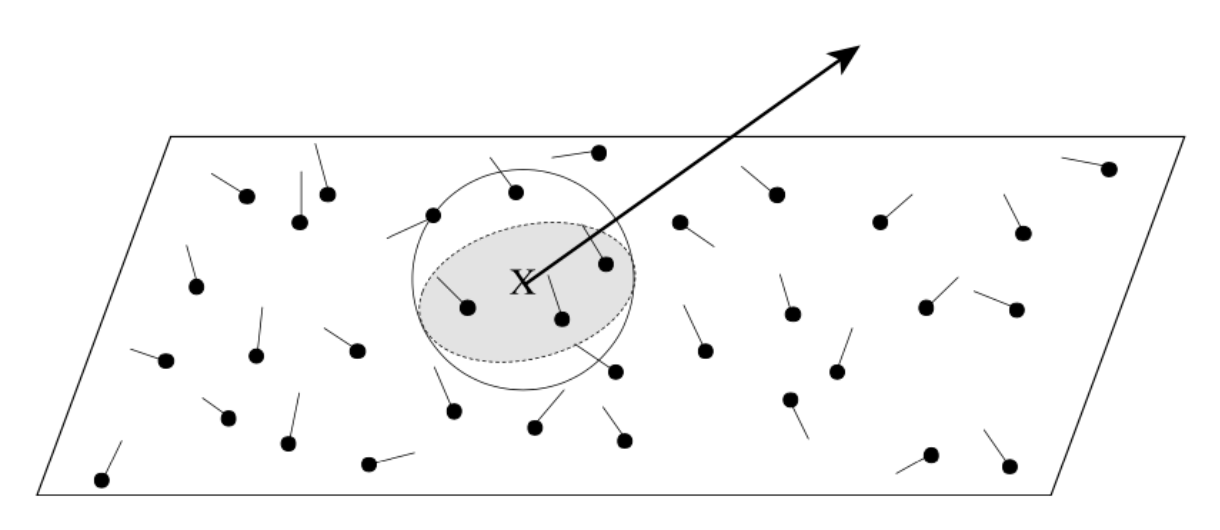
光子映射的计算方法是局部密度估计(local density estimation)。

• 思路：区域内光子数越多，该区域就越明亮
• 对于每一个着色点，找到 N 个离其最近的光子，将光子所在表面区域圈起来

Vertex Connection and Merging (VCM)⚓︎

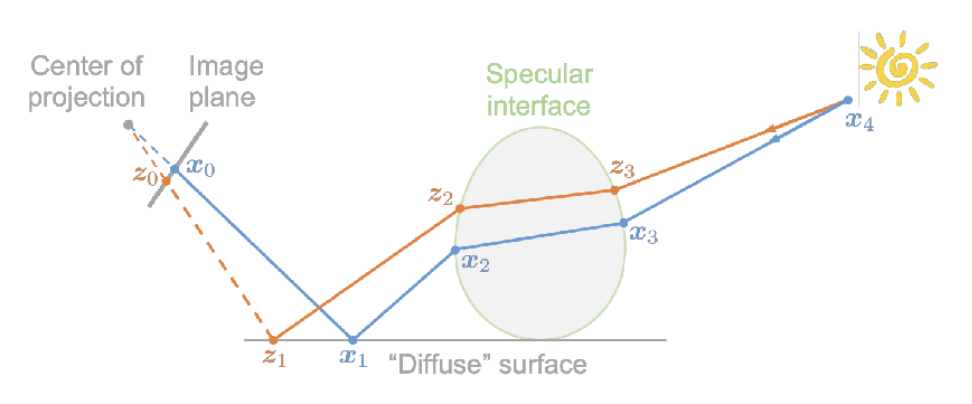
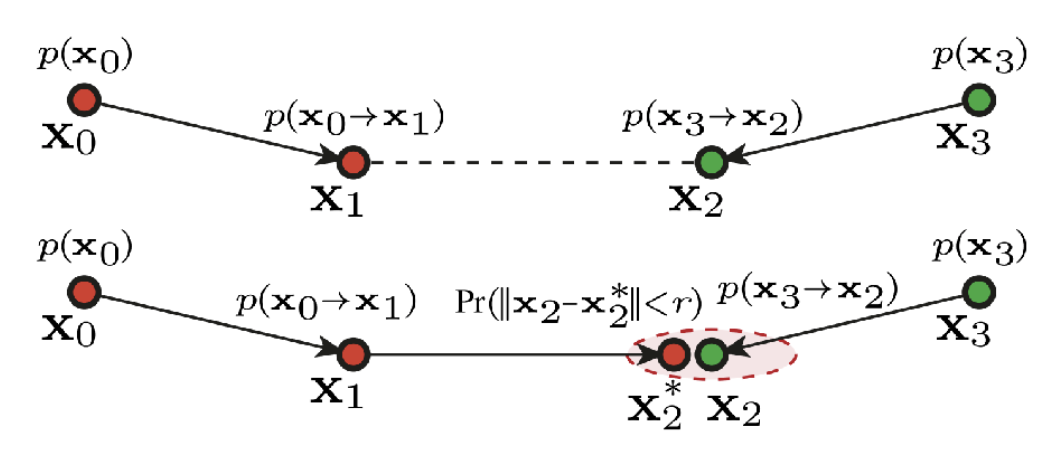
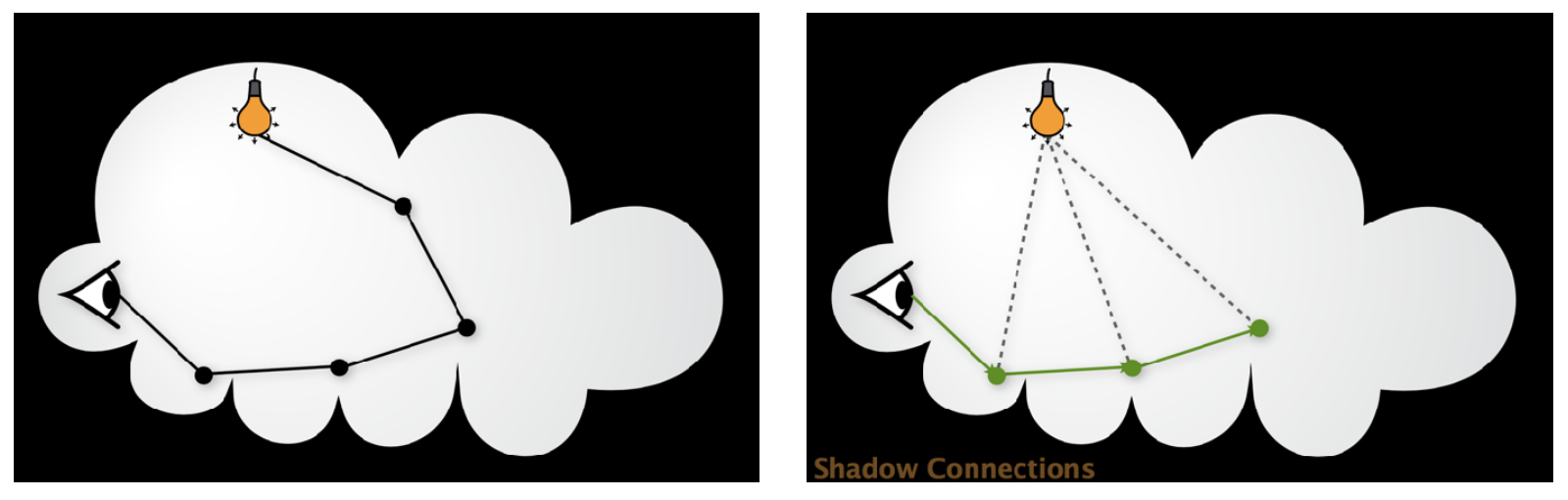
顶点连接与合并(vertex connection and merging, VCM) 是对 BDPT 和光子映射这两个方法的结合。它的关键思路是：

• 对于在 BDPT 中那些端点不能连接，但可以合并的半路径，不要直接丢掉
• 使用光子映射来处理这些可以合并的邻近“光子”

上图对应可连接的情况，下图对应不可连接，但可合并的情况。

Instant Radiosity⚓︎

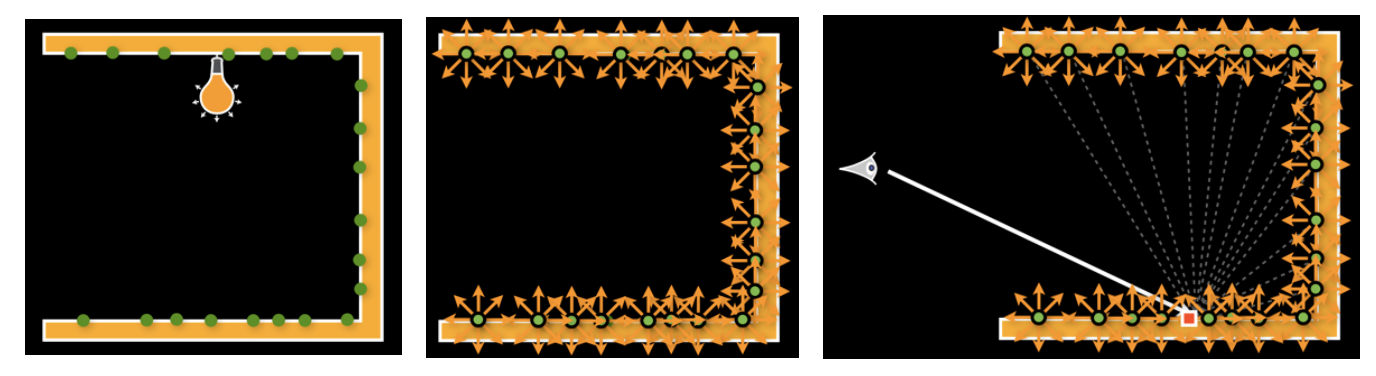
实时辐射度(instant radiosity)（有时又称多光方法）的思路是：被照亮的表面也可看作是光源。具体来说：

• 从光源处发射光线半路径，并假设每个半路径的端点是一个虚拟点光源(virtual point light, VPL)
• 使用 VPLs 渲染场景，就和往常一样

缺点

• 当 VPLs 靠近着色点时，就会出现莫名的光点（尖刺 (spike)）
  • 解释：在路径追踪的渲染方程中，我们将对立体角的采样转化为对面积的采样，此时方程中还包含除以距离平方项。当两点间距很小时，结果值就会很大，因此会出现这些莫名的亮点
• 无法处理光泽材质

Advanced Appearance Modeling⚓︎

Non-surface Models⚓︎

Participating Media⚓︎

例子

雾云

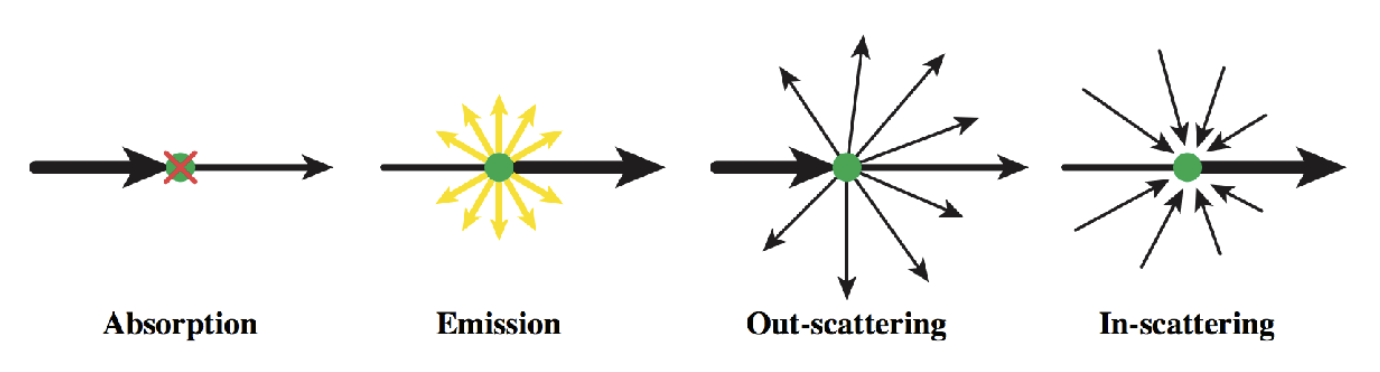
在光线穿过参与介质(participating media) 的过程中，任何时刻都可能（部分）被吸收和散射。

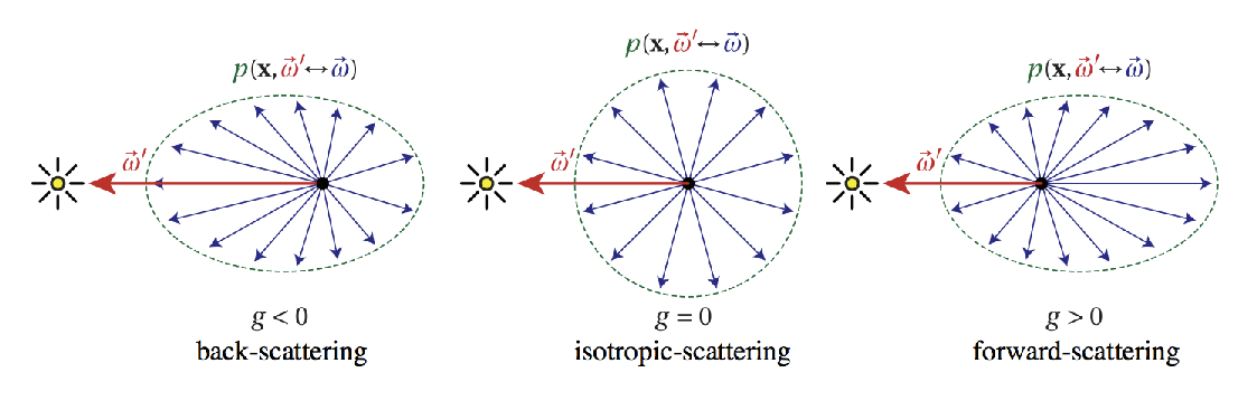
使用相位函数(phase function) 来描述参与介质中任意点 x 处光散射的角分布。

参与介质在渲染中的应用：

• 随机选择一个弹射方向
• 随机选择一个直行距离
• 在每个着色点上连接光线

一些应用

例 1 例 2 例 3

电影《超能陆战队》

游戏《刺客信条：枭雄》

论文：Augmented MPM for phase-change and varied materials

Hair / Fur / Fiber (BCSDF)⚓︎

像头发这样的材质在 CG 中是如何渲染的呢？

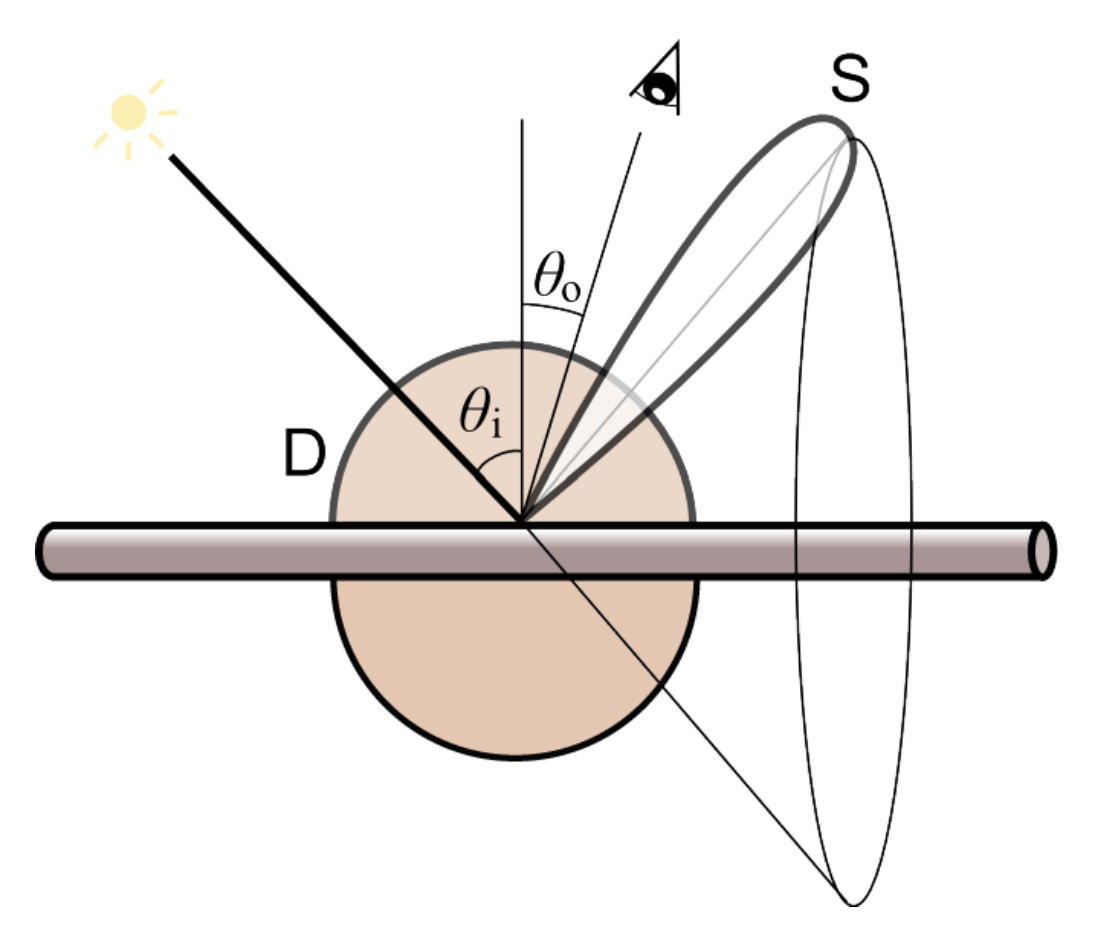
一种简单的模型叫做 Kajiya-Kay 模型。它把一根头发丝当做一根圆柱，打在圆柱上的光线会散射出去，其中大部分散射光线会形成一块圆锥区域。

渲染效果

看起来一般般，一看就知道是假的。

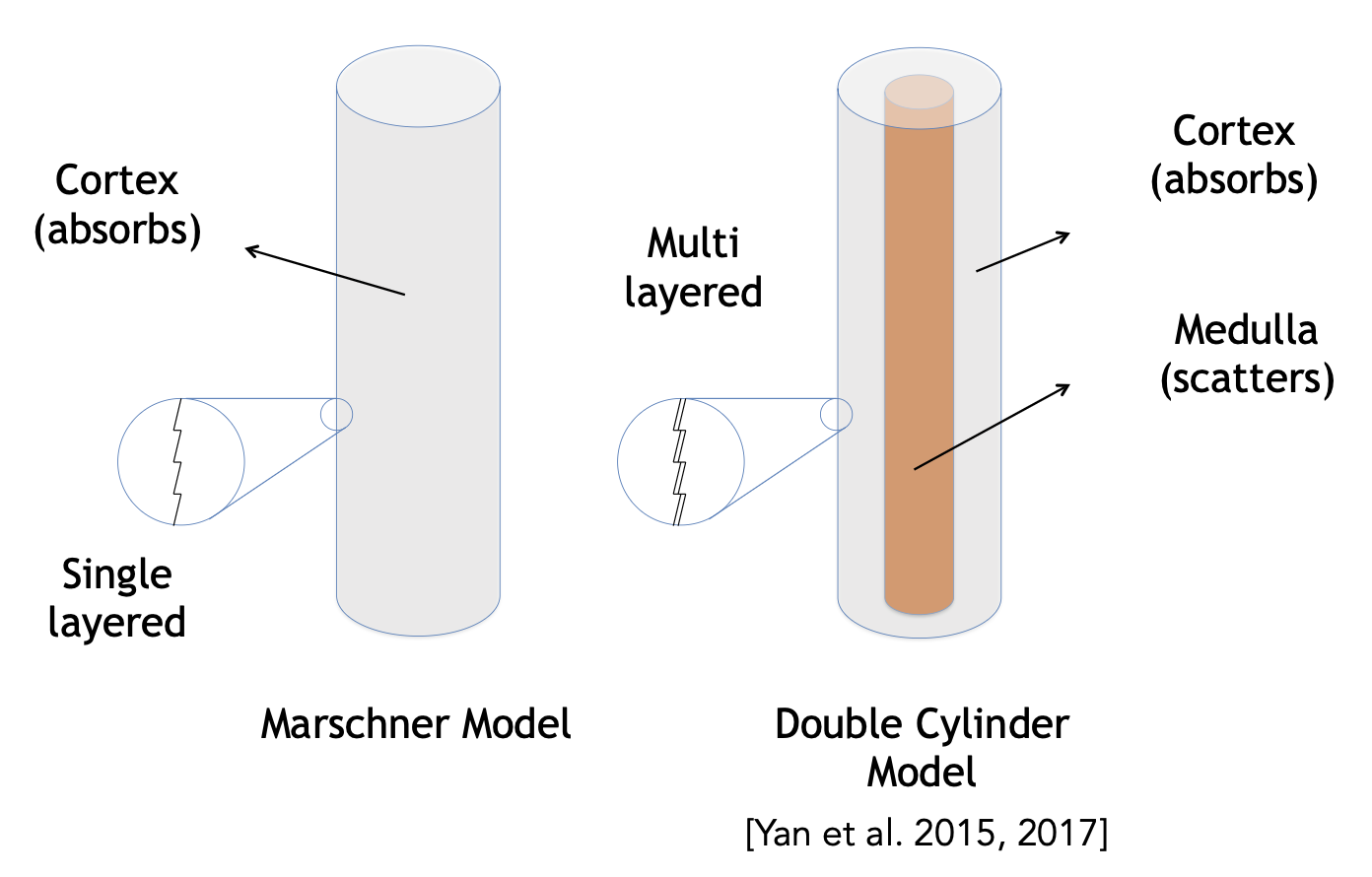
于是有人提出了更复杂的模型，叫做 Marschner 模型。相比前面 Kajiya-Kay 模型，它有了以下改进点：

• 圆柱表面不再是平整的，而是锯齿状的
• 更具体地，把圆柱看成是一根玻璃柱，因此打在头发丝上的光还会穿过去

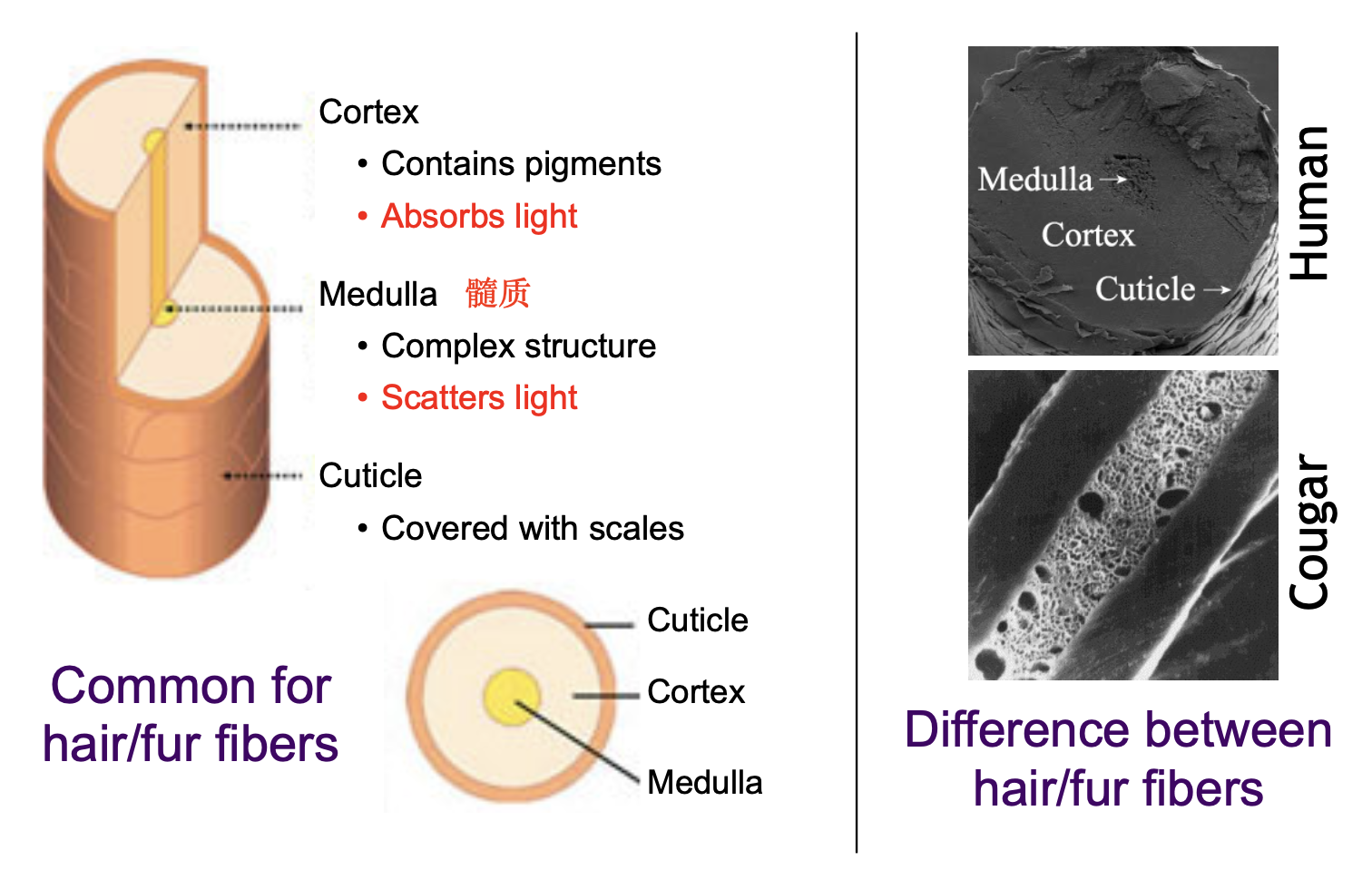
我们一般称这个圆柱的表面和内部分别为表皮(cuticle) 和皮质(cortex)。

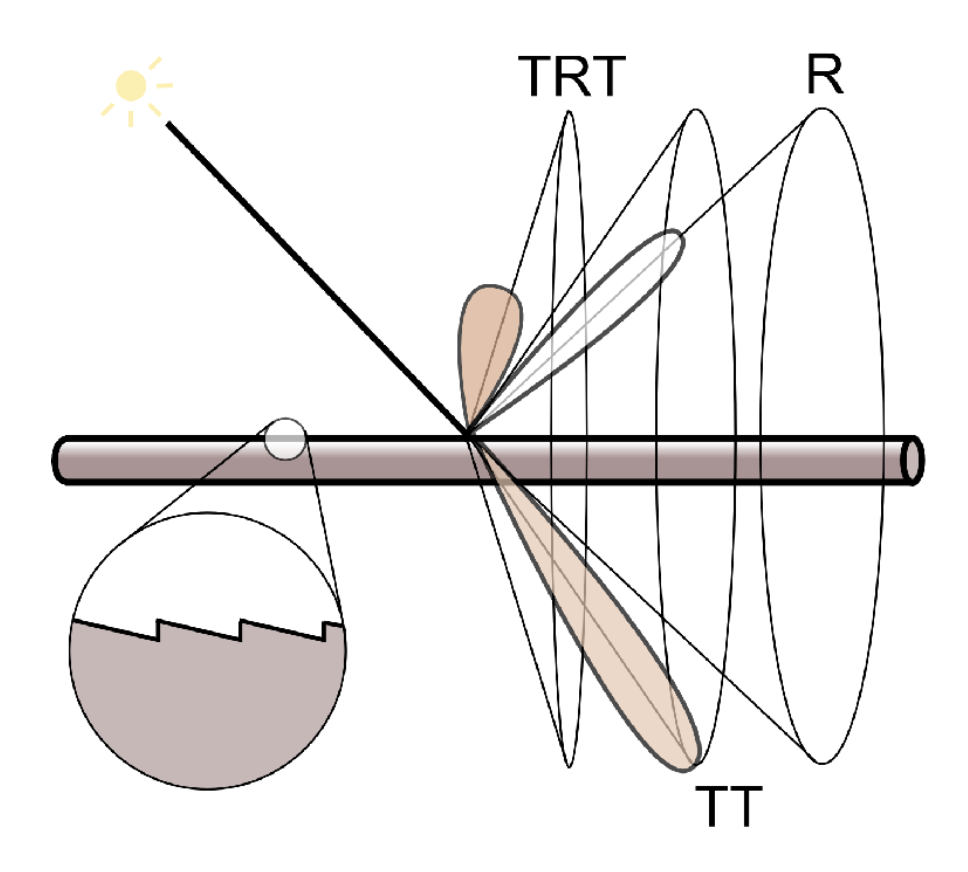
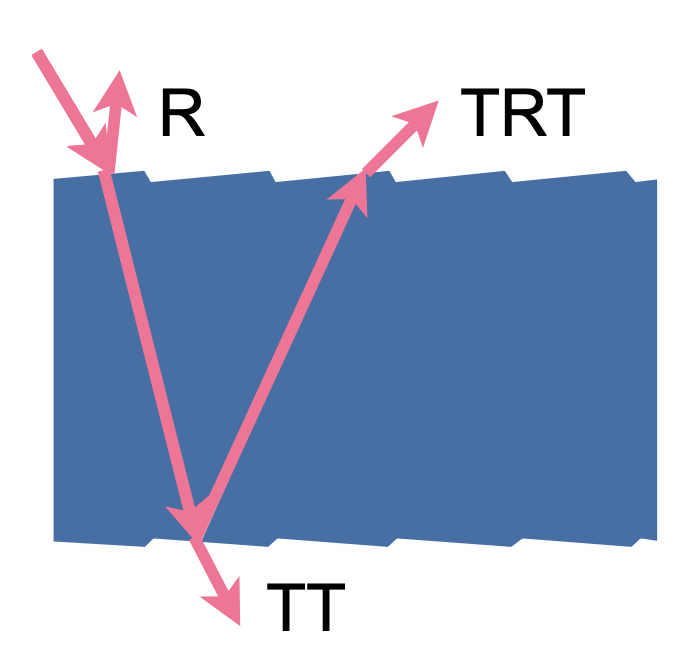
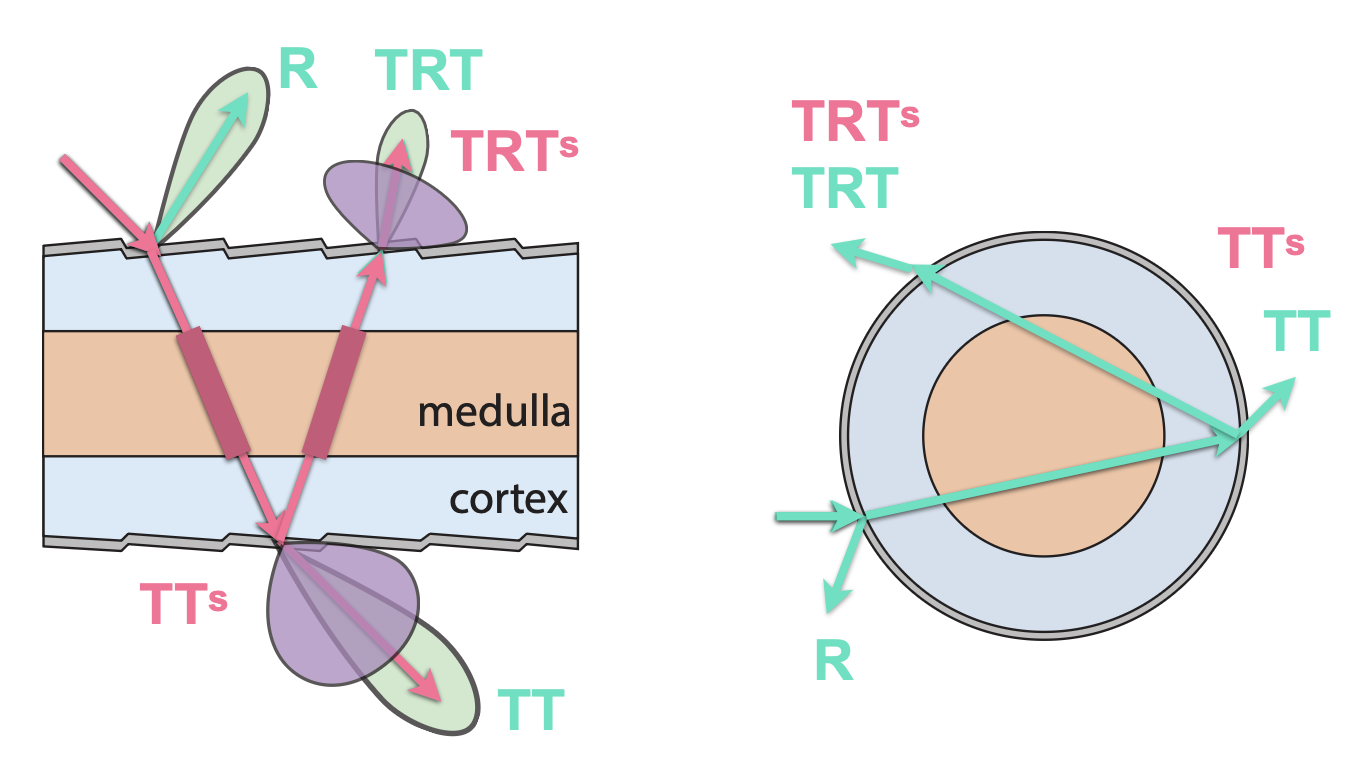
由于其特殊构造，所以和光线的交互要分为 3 种情况：

• R：直接在上表面反射
• TT：光线穿过上下表面
• TRT：光线穿过上表面后，在下表面反射，最后从上表面出去

R：发射 (reflection)，T：透射 (transmission)（折射）

渲染效果

比前一个模型看起来好多了。

头发外观模型的应用

例 1 例 2

杀马特发型

游戏《最终幻想 15》

动画《疯狂动物城》

如果直接拿渲染头发的技术渲染动物毛发的话，得到的结果并不理想，动物毛发的那种扩散和饱和的外观就无法呈现出来。

在生物学中，毛发除了有表皮和皮质外，内部还有一个叫髓质(medulla) 的东西。并且人的毛发和其他动物的毛发的髓质大小是不同的：

渲染效果（从中感受到引入髓质的重要性）

例 1 例 2

从左往右，髓质大小不断增加。

由于考虑了髓质的存在，所以原来的单个的柱体模型就要进化为双柱体模型(double cylinder model) 了。

与光线的交互也变得更复杂了：

应用

例 1 例 2 例 3

Granular Material⚓︎

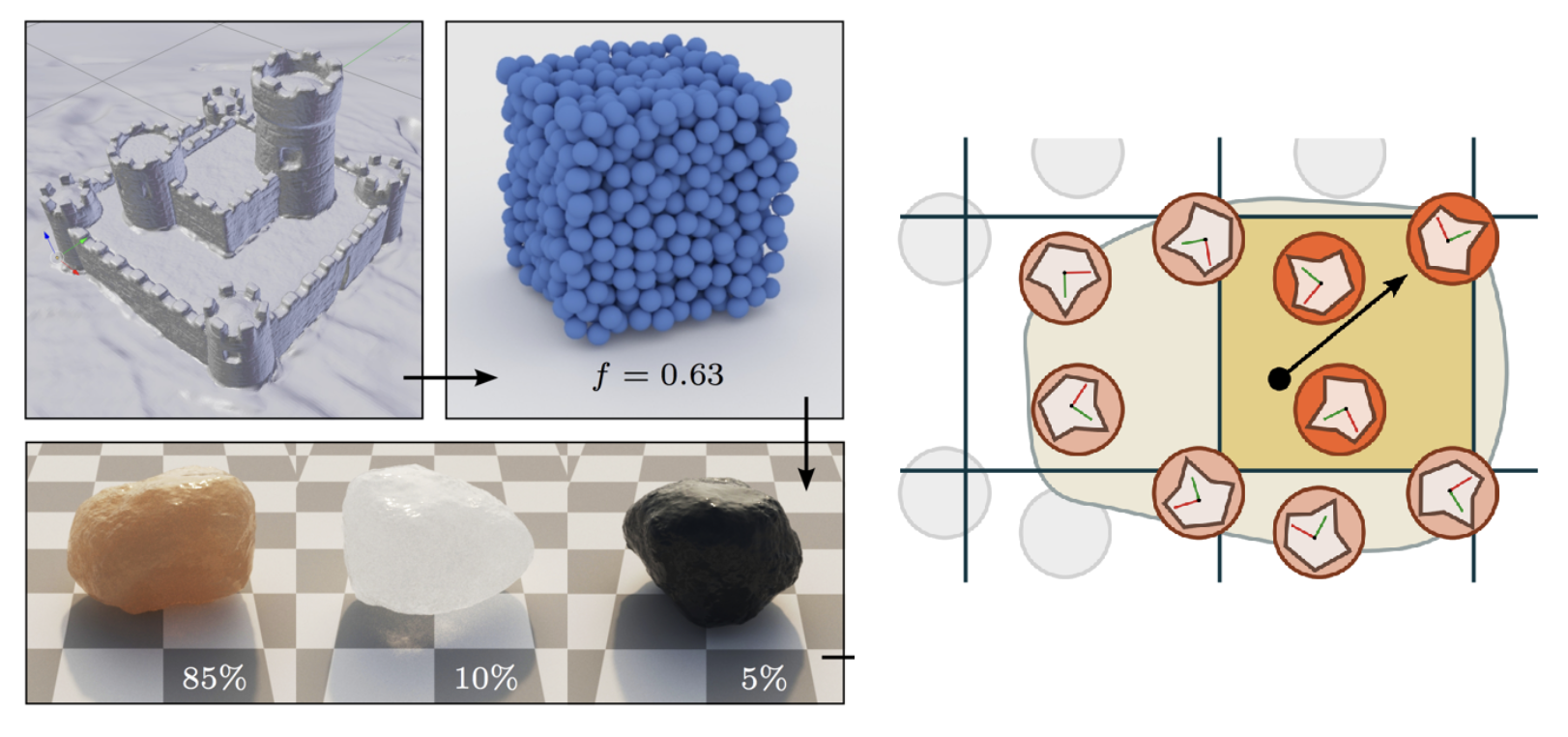
下面这些都属于颗粒材质(granular material)：

显然，如果直接为每个颗粒建立单独的模型，那计算量也太大了。我们可以采用过程(procedure) 定义的方法避免这一问题。

渲染效果

例 1 例 2

皮克斯动画《Piper》

Surface Models⚓︎

Translucent Material (BSSRDF)⚓︎

以下物体均属于半透明材质(translucent material)：

例子

例 1 例 2

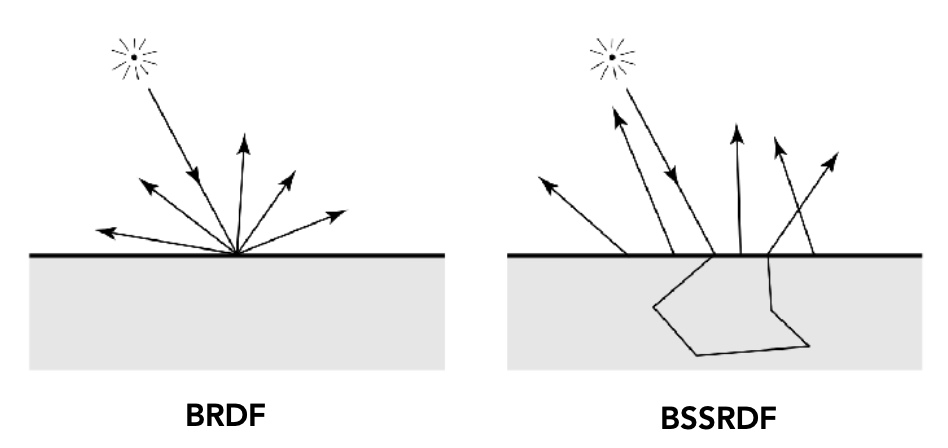
次表面散射(subsurface scattering)：许多表面的视觉特性，源于光线出射点与入射点的不同。

• 但这违反了 BRDF 的基本假设（BRDF 假设入射点和出射点是同一个点）

  

所以就有了在 BRDF 基础上泛化的散射函数 BSSRDF \(S(x_i, \omega_i; x_o, \omega_o)\)：某个点的出射辐照度源于另一点的入射微分辐照度。于是也就有了对原有渲染方程的泛化——在所有点和所有方向上做积分，得到： $$ L(x_o,\omega_o)=\int_A\int_{H^2}S(x_i,\omega_i,x_o,\omega_o)L_i(x_i,\omega_i)\cos\theta_i\mathrm{d}\omega_i\mathrm{d}A $$

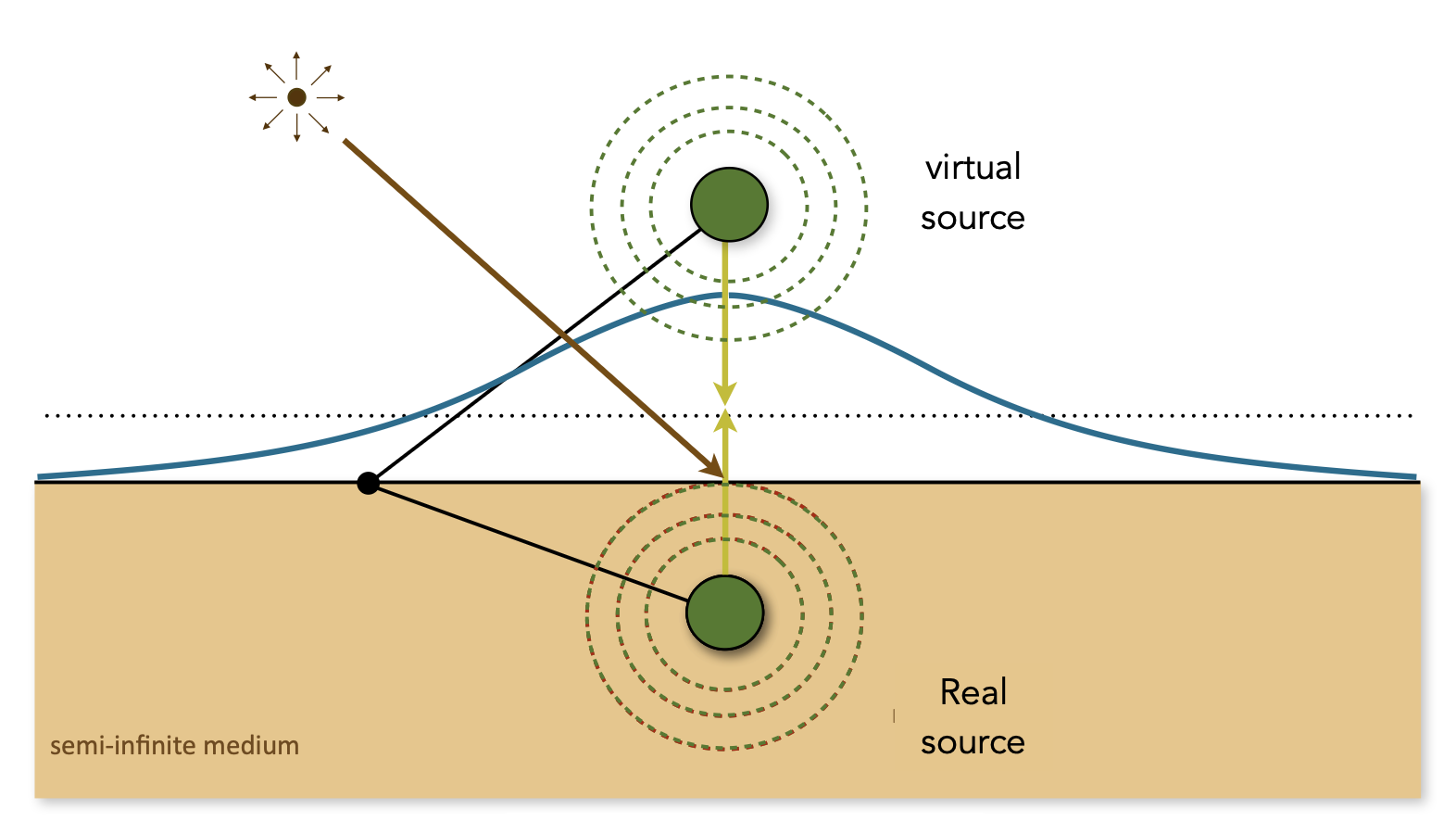
由于直接计算 BSSRDF 相当复杂，人们就想出一些近似算法来表现次表面散射。其中一种方法叫做偶极近似(dipole approximation)，它通过引入两个点光源来近似模拟光的扩散。

• 举一个生活中常见的例子：用手遮挡手电筒的光，你会发现光会穿透那只挡光的手，就好像光源来自手心一样

例子

例 1 例 2 例 3 例 4

这些都是用电脑渲染出来的假人：

Cloth⚓︎

布料(cloth) 由缠绕在一起的纤维构成。“缠绕”分为两级：

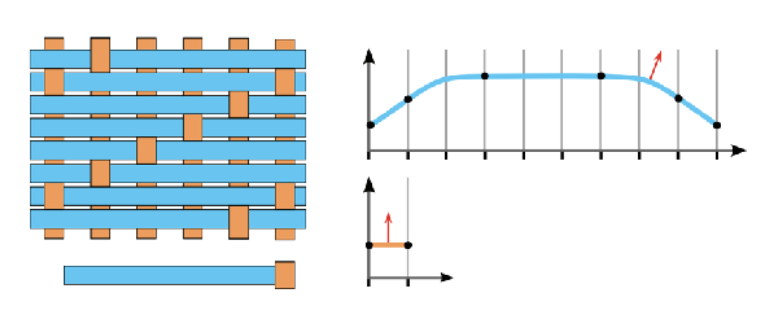
下面两张图分别展示了编织 (woven) 和针织 (knitted) 的布料：

将布料作为表面渲染时，需要根据给定的编织模式来计算整体的表现。这里就不展开介绍细节内容了。

使用 BRDF 的渲染结果

这种渲染方式的缺点是没法渲染像天鹅绒这样的布料，它的纤维是朝外分布的，很难用 BRDF 来表示。

一种解决方案是将布料作为参与介质来渲染。

• 单根纤维的特性及其分布 -> 散射参数
• 把织物看作空间中分布的体积，可以将这块体积划分为超级细小的格子，每个格子中纤维的朝向分布是已知的，类似渲染云雾
• 但计算量很夸张 ...

另一种方案是按真实纤维来渲染（计算量也很夸张）：

例子

例 1 例 2

没找到原论文 QAQ

迪士尼动画《圆梦巨人》（2016）

Detailed Material (Non-Statistical BRDF)⚓︎

有时用计算机渲染出来的东西可能过于完美，反而看起来不像真的。

现实世界的情况会更加复杂，因此反而不存在完美的物体。

例子

微表面模型更真实的细节

通过微表面模型渲染的物体过于完美，缺少真实感。

加入更真实的划痕等贴图后，水壶看起来就更像真的。

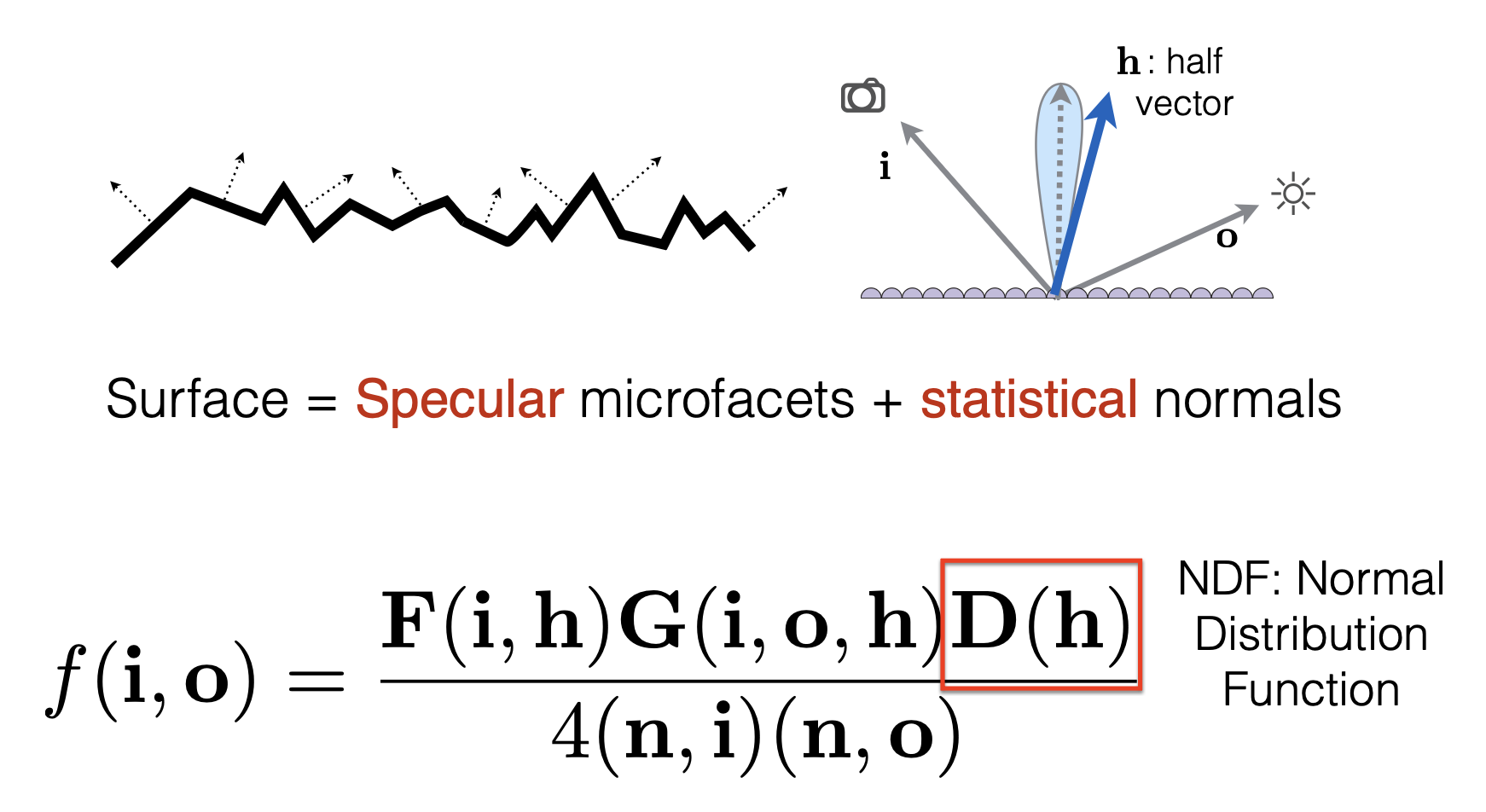
回忆一下微表面上 BRDF 的计算：

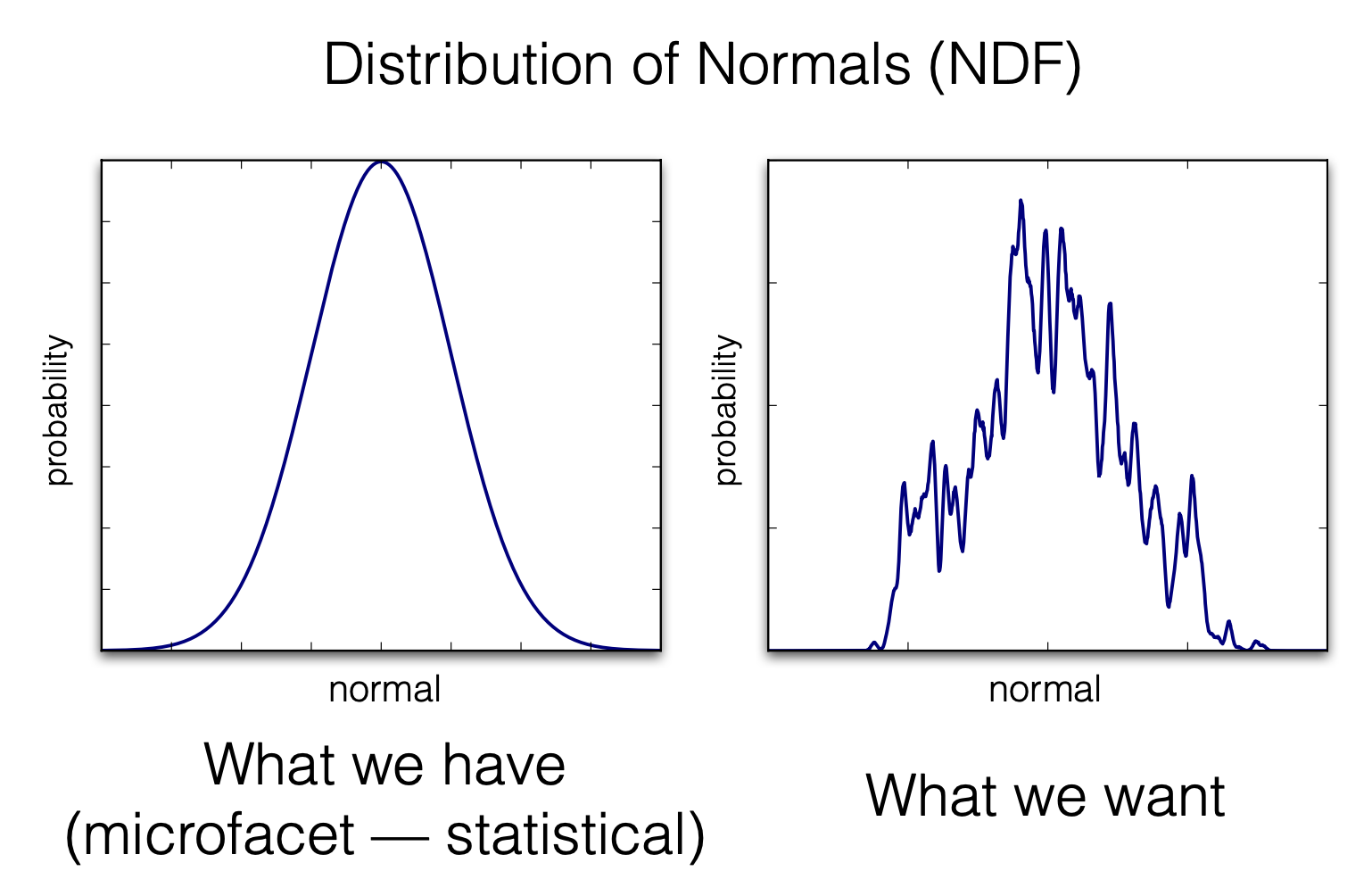
在微表面模型中，我们假设法线分布函数（NDF）是一个高斯函数，但实际的 NDF 并不会这么理想：

我们可通过各向同性的法线贴图来增加这些看似真实的细节。

加入亮片后让物体表面更好看些：

然而，如果直接用这种方式渲染，计算量相当大，耗时会非常久。

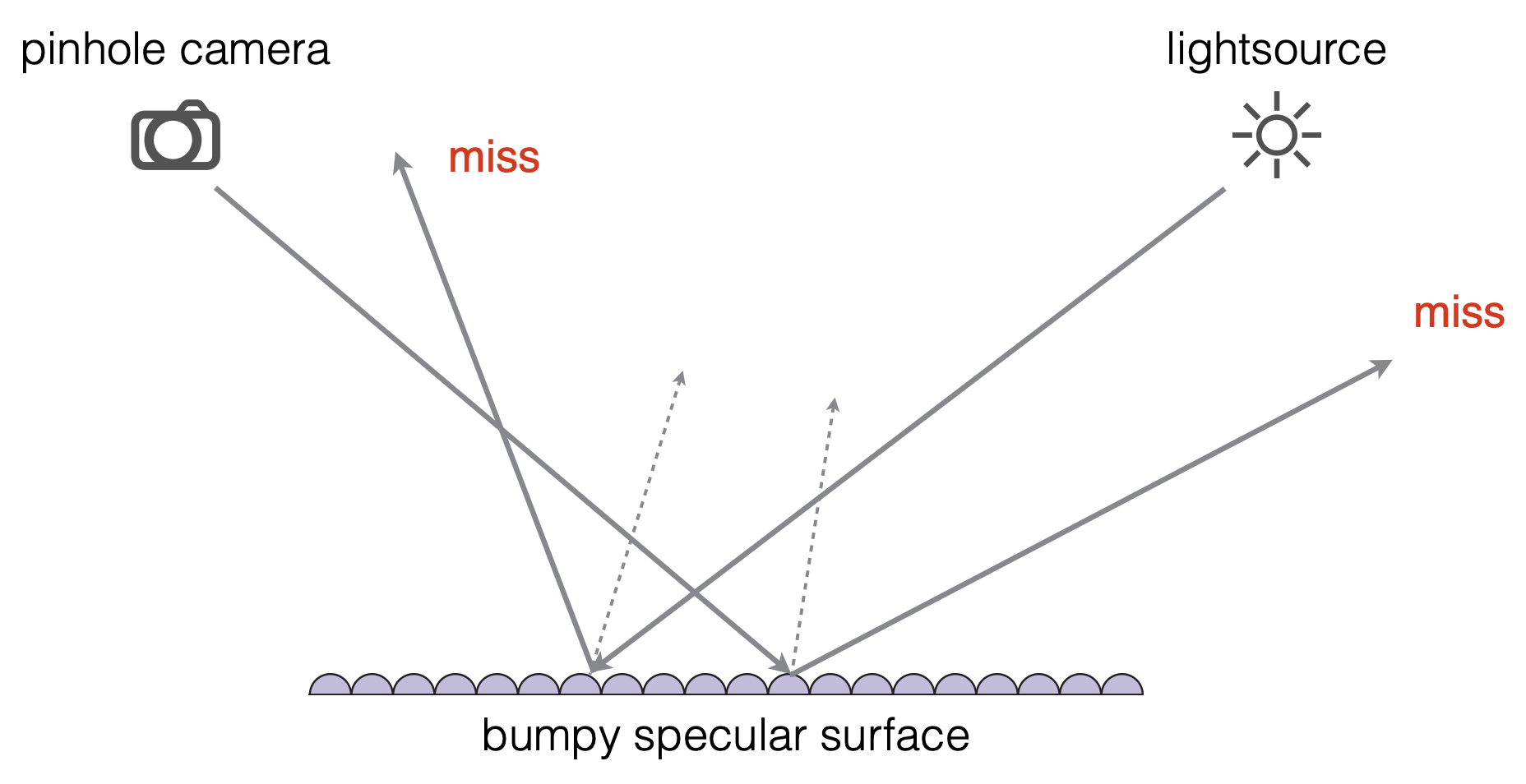
之所以计算量大，是因为加入法线贴图后，物体表面变得凹凸不平（在原先的微表面模型中，我们假设物体表面（从宏观角度看）是平整的），因此会出现光源发出的路径打不到相机，或者相机发出的路径打不到光源的情况。

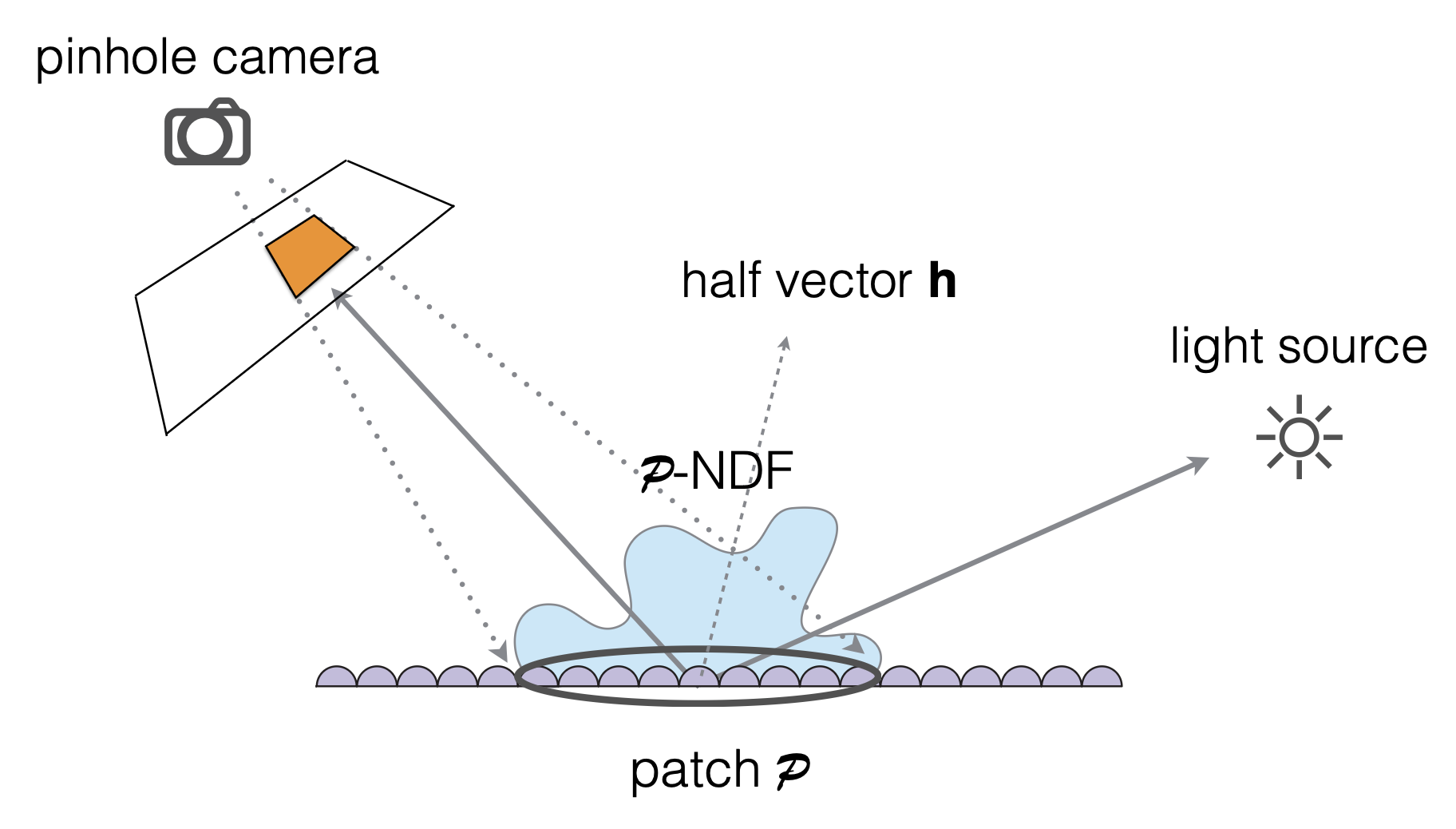
解决方案是将在一个像素范围内进行 BRDF 的计算。一个像素会覆盖多个微表面，然后把这块区域内的微表面分布拿出来，计算其法线分布，以替代原本在光滑平面上的法线分布。

如图所示，覆盖的微表面越多，\(\mathcal{P}\)-NDF 分布就越符合统计规律：

各种法线贴图对应的 \(\mathcal{P}\)-NDF 的形状：

例子

例 1 例 2 例 3

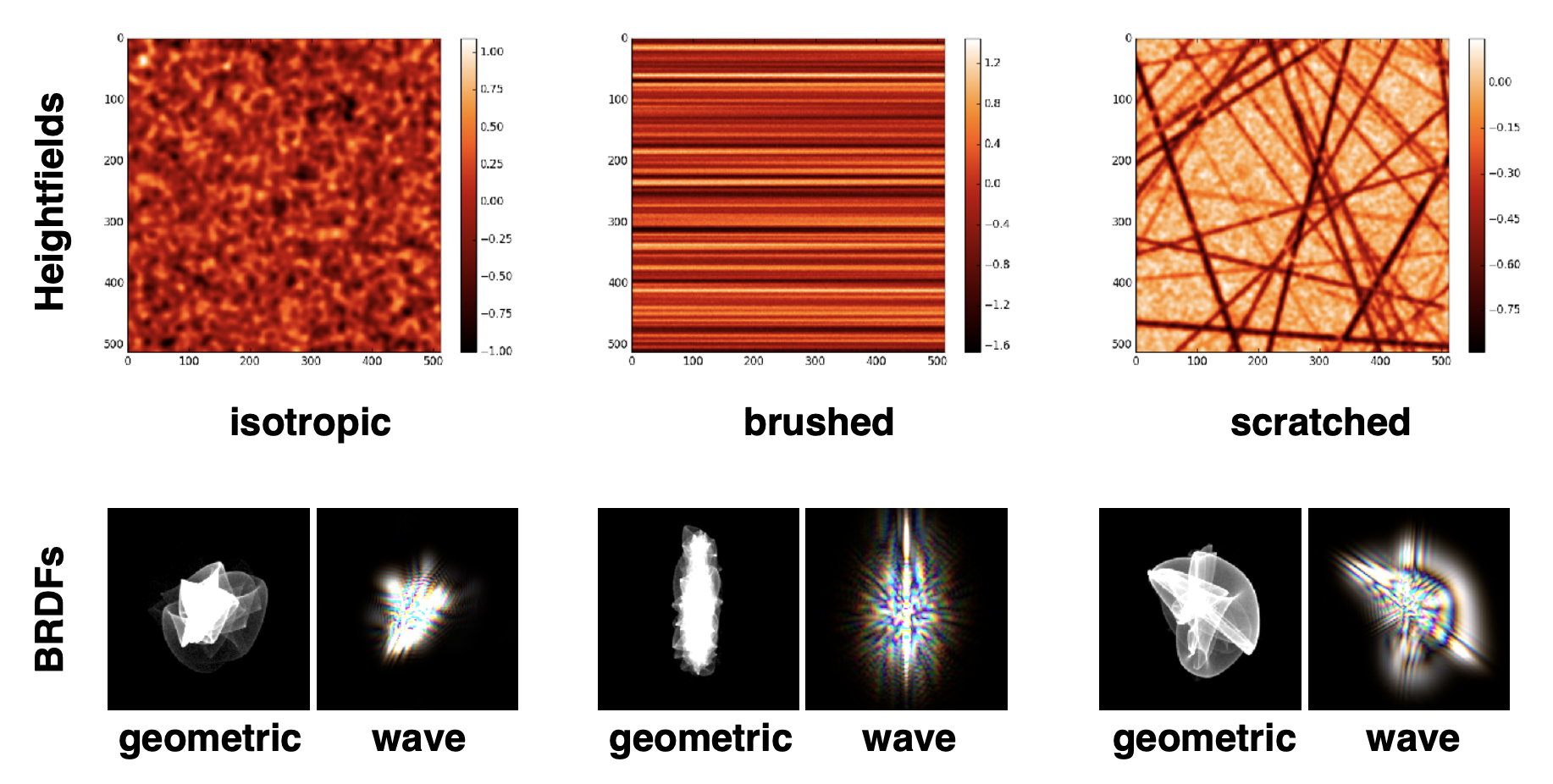
Wave Optics⚓︎

最近的一种趋势是将波动光学(wave optics) 应用到 CG 中。由于光是一种波，所以会有干涉、衍射之类的现象，而这些现象会影响到物体的细节表现。

根据我们生活中的观察，一些看起来是单色的物体，凑近了看（或者拍下照片放大了看）会发现各种彩色的点。

波动光学下的材质细节：

由于背后涉及到的物理知识过于复杂，所以这里不会展开讨论。

应用

例 1 例 2

Procedural Appearance⚓︎

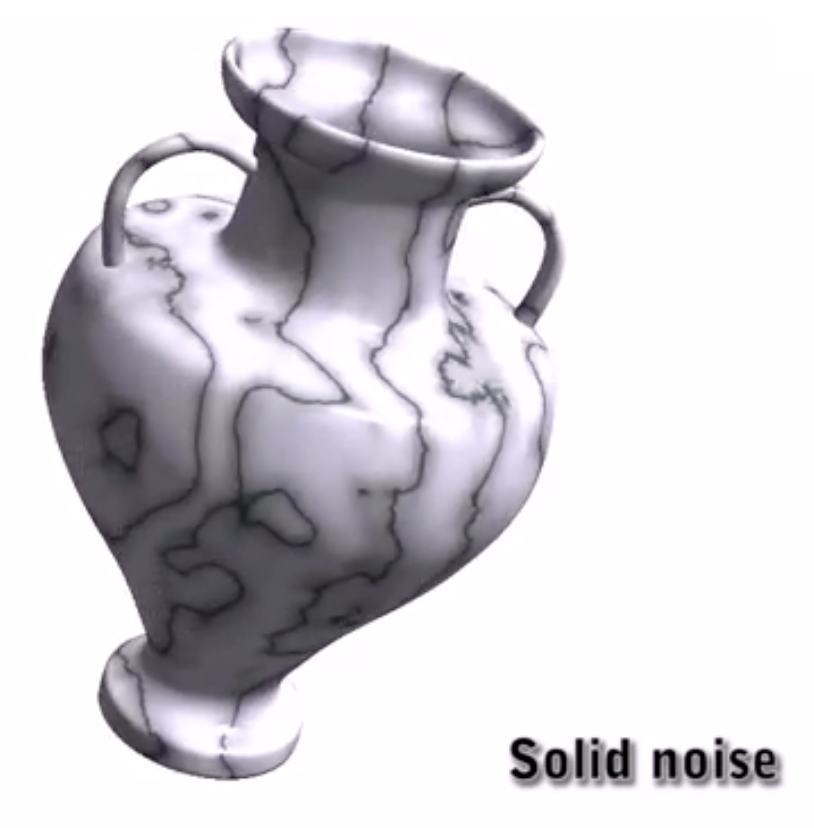
我们可以不用纹理来表现物体细节，而是通过实时计算一个噪声函数来实现。

对于 3D 的噪声函数，即便将物体切开来，依然能看到表面细节。

我们还可以通过设置阈值的方式来构建一个二元噪声函数，比如下图汽车上的铁锈：

应用

例 1 例 2 例 3 例 4

评论区