Image Matching and Motion Estimation⚓︎
约 2743 个字 预计阅读时间 14 分钟
Image Matching⚓︎
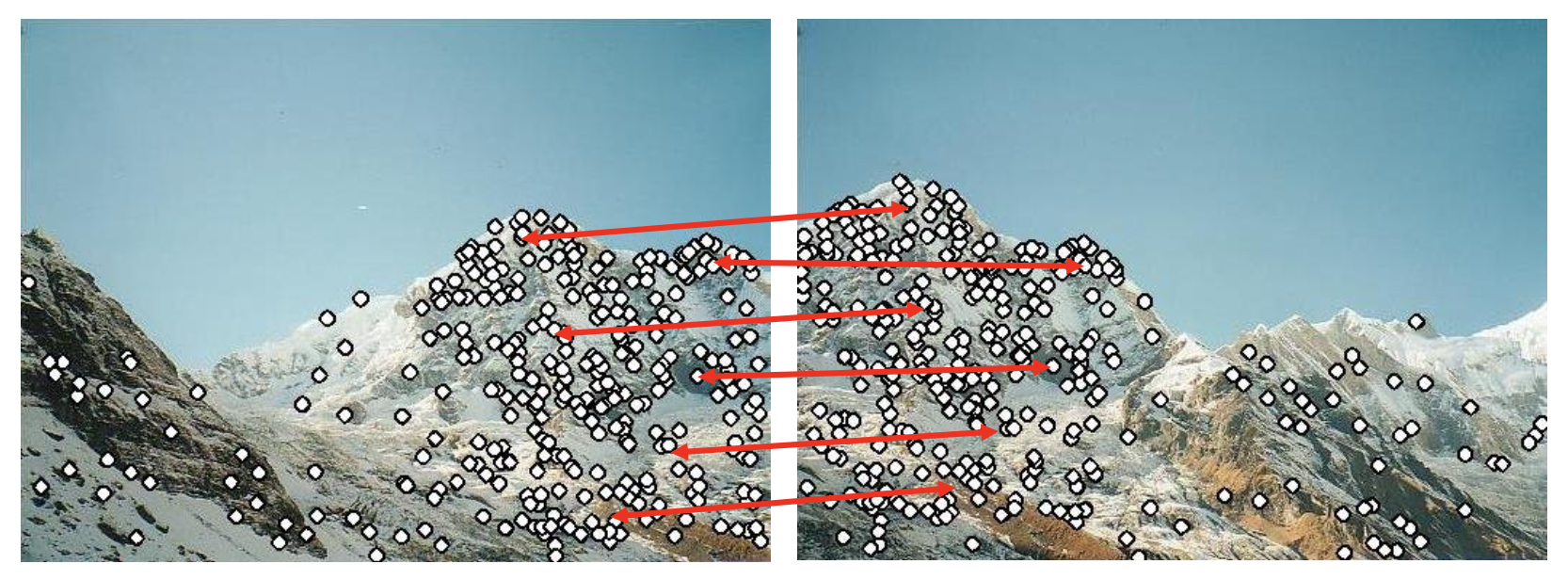
特征匹配(feature matching):寻找两图像之间点到点的对应关系。
特征匹配有着大量应用:
-
图像对齐 (image alignement)/ 拼接 (stitching)
-
3D 重构
-
运动追踪 (motion tracking)
-
物体识别
-
索引和数据库检索
- 机器人导航
- ...
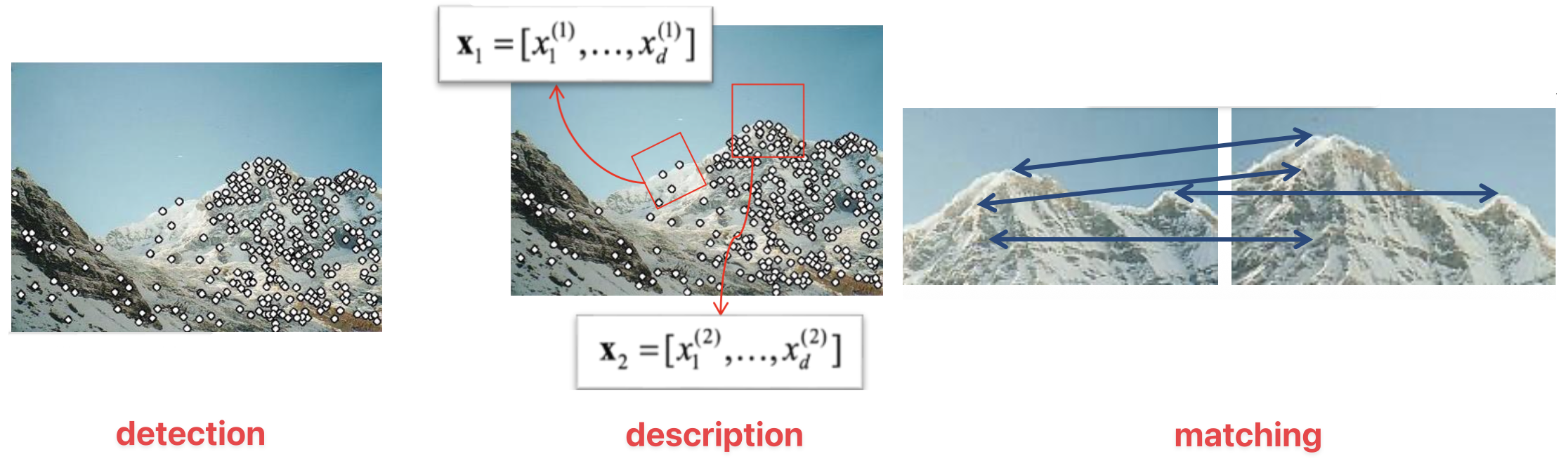
特征匹配的组成部分:
- 检测(detection):识别图像上的兴趣点(interest point)/ 特征点
- 描述(description):围绕每个兴趣点,提取向量特征描述符 (descriptor)
- 匹配(matching):确定两个视图下描述符间的对应关系
Detection⚓︎
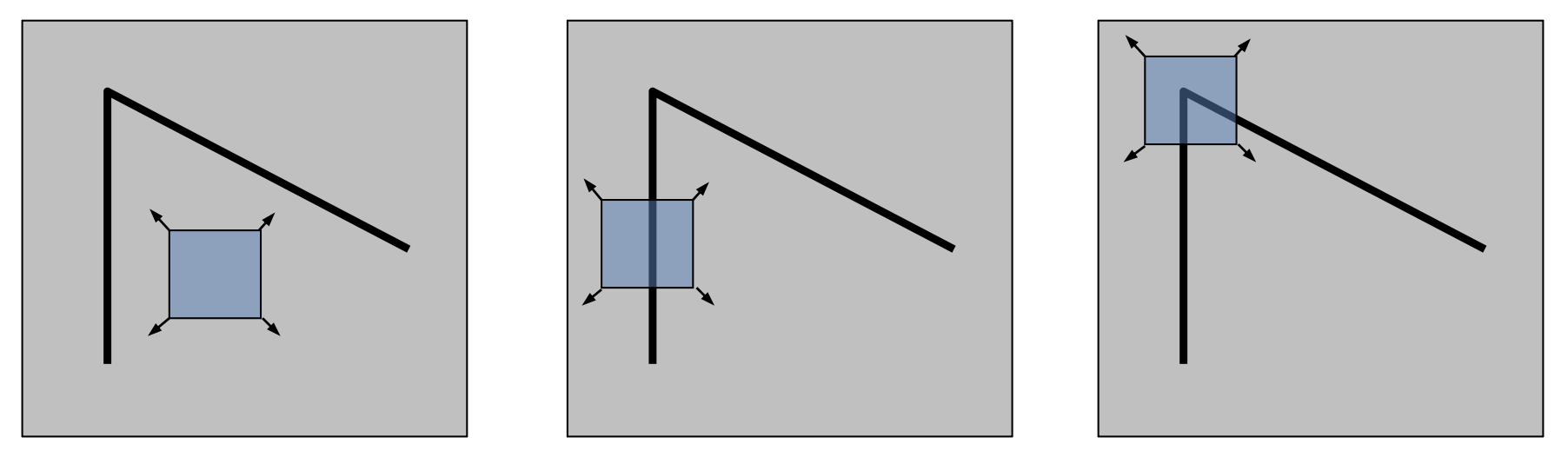
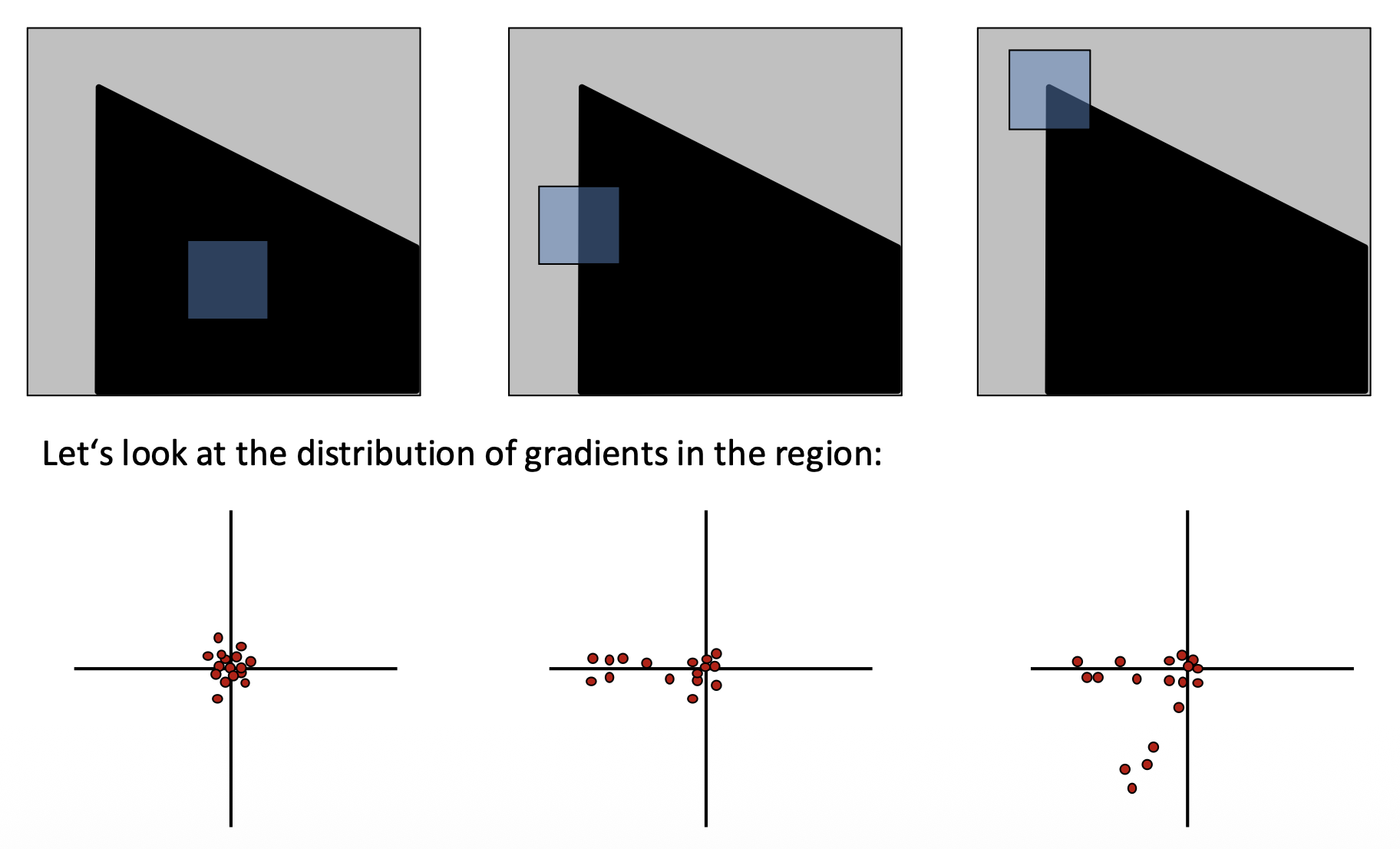
我们对图像上独一无二的部分更感兴趣,这些部分将和其他图像形成无歧义的匹配。那么这个“唯一性(uniqueness)”该如何定义呢?一种对唯一性的局部测量方法是在图像上选取一个窗口区域,以任意方向移动这个窗口,找到窗口内像素变化较大的地方。
- 平滑(flat) 区域:沿任意方向都不会改变
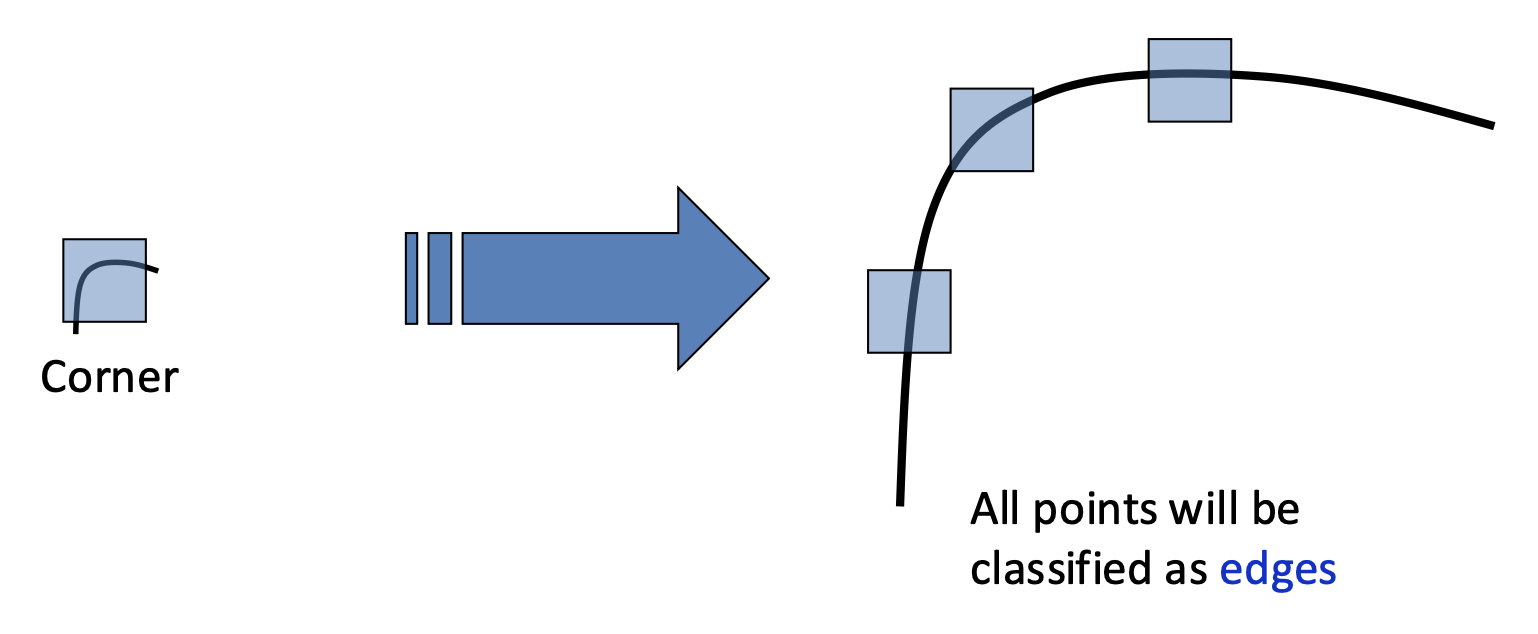
- 边(edge):沿着边的方向不会改变
- 角(corner):沿任意方向都会有显著变化
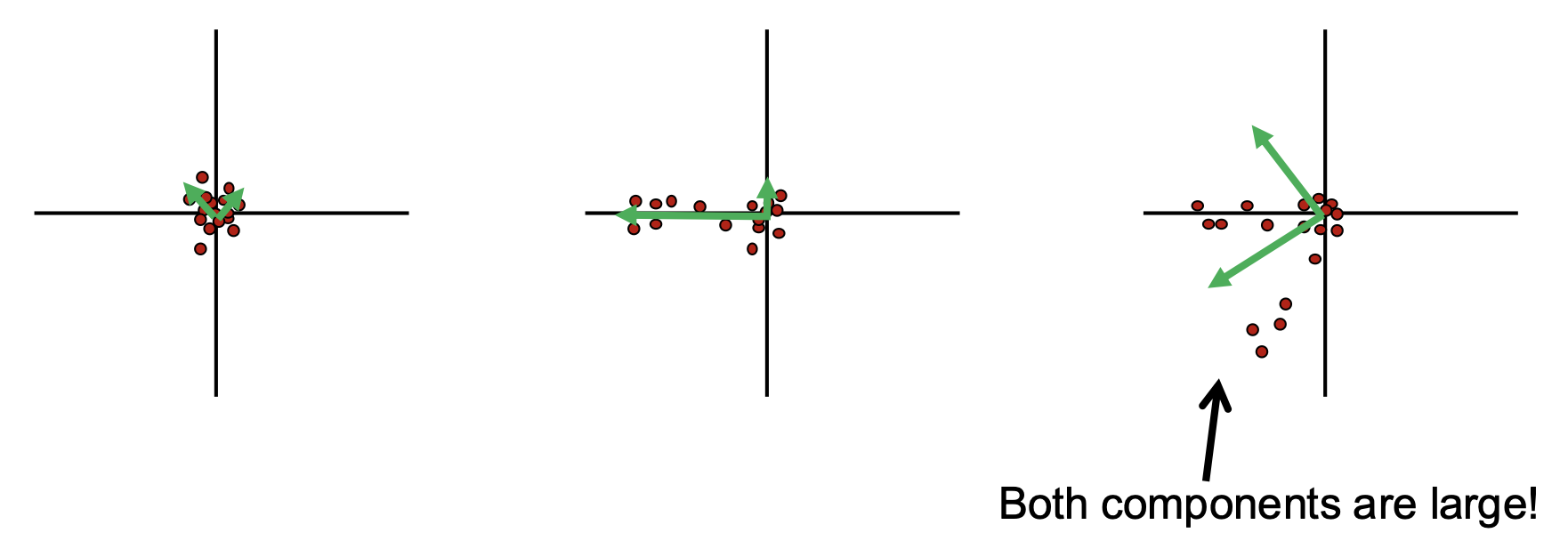
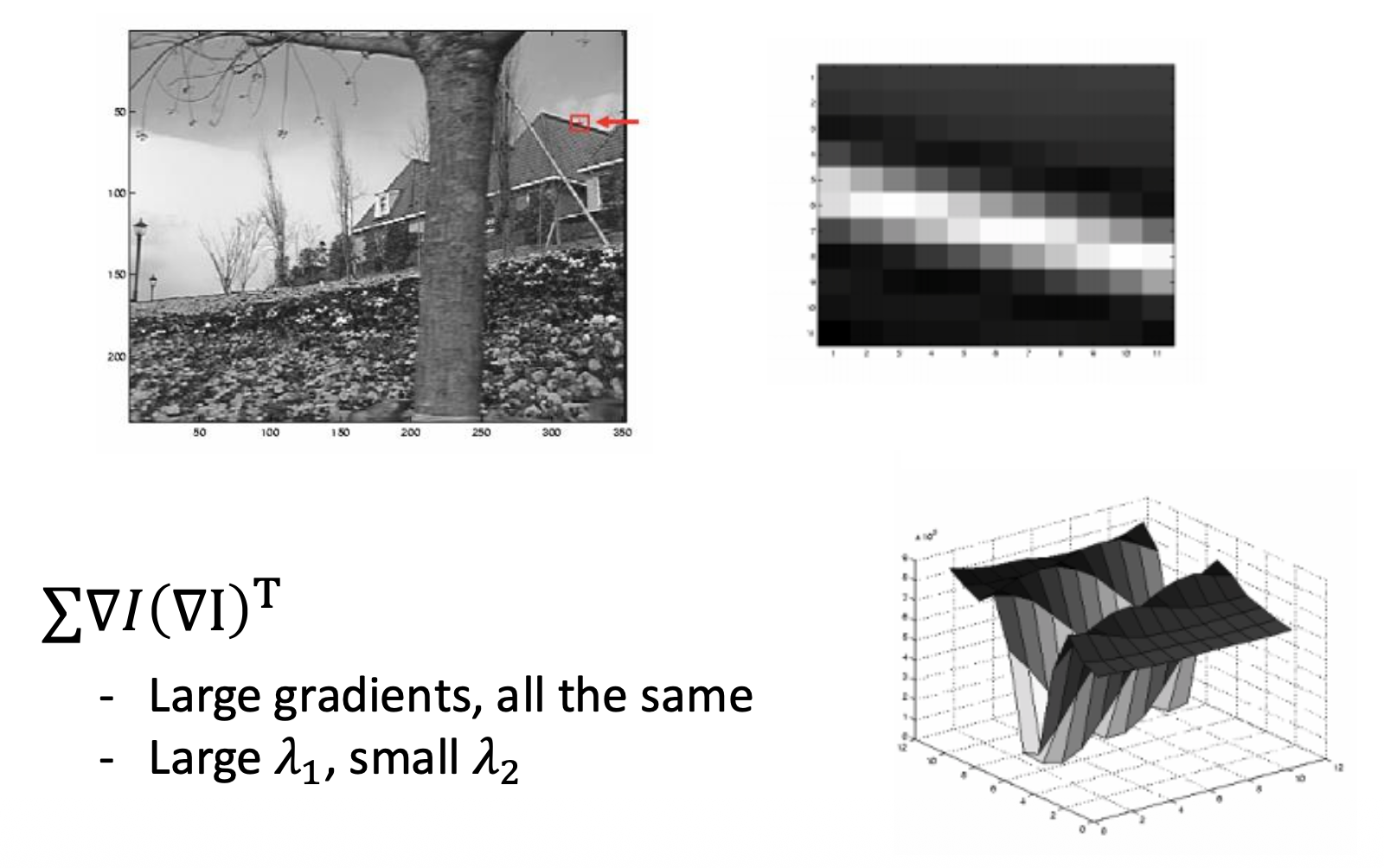
放大上面的图片,来看一下这些区域附近的梯度分布:
主成分分析(principal component analysis):
- 第一主成分是方差最大的方向
- 第二主成分是与前一个成分正交,且具有方差最大的方向
角检测的步骤:
-
计算每个点的协方差矩阵
\[ H=\sum_{(u,v)}w(u,v)\begin{bmatrix}I_x^2&I_xI_y\\I_xI_y&I_y^2\end{bmatrix}\quad I_x=\frac{\partial f}{\partial x},I_y=\frac{\partial f}{\partial y} \]其中 \(w(x, y)\) 一般为高斯权重(Gaussian weights)
-
计算特征值
\[ H=\begin{bmatrix}a & b\\c & d\end{bmatrix}\quad\lambda_{\pm}=\frac{1}{2}\left((a+d)\pm\sqrt{4bc+(a-d)^2}\right) \] -
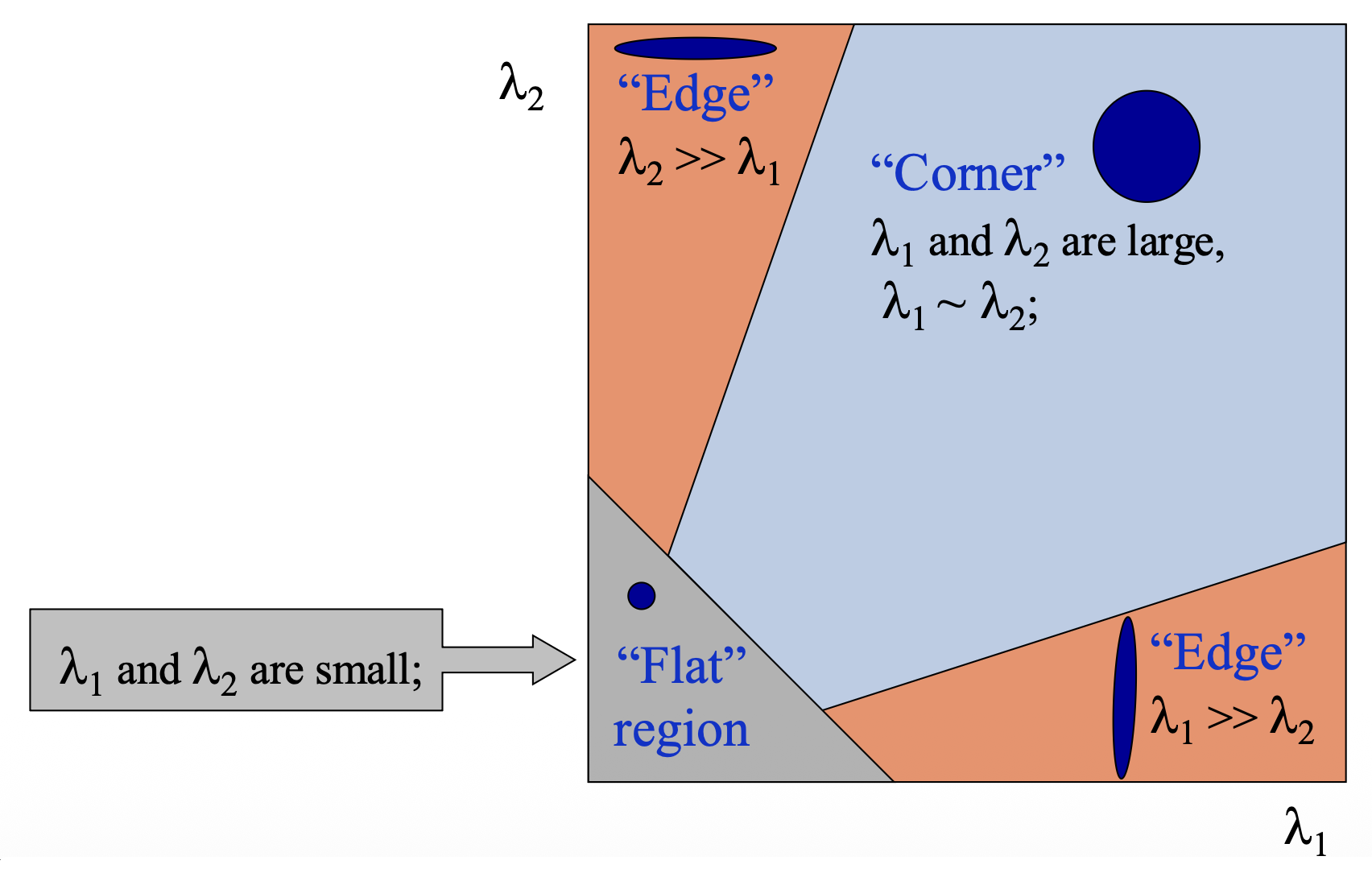
使用 \(H\) 的特征值对点分类
Harris Detector⚓︎
哈里斯角检测器(Harris corner detector) 计算以下响应函数: $$ f=\frac{\lambda_1\lambda_2}{\lambda_1+\lambda_2}=\frac{determinant(H)}{trace(H)} $$
\(f\) 被称为角响应值(corner response)。
计算过程如下:
- 计算每个像素的导数
- 计算每个像素周围高斯窗口内的协方差矩阵 \(H\)
- 计算角响应函数 \(f\)
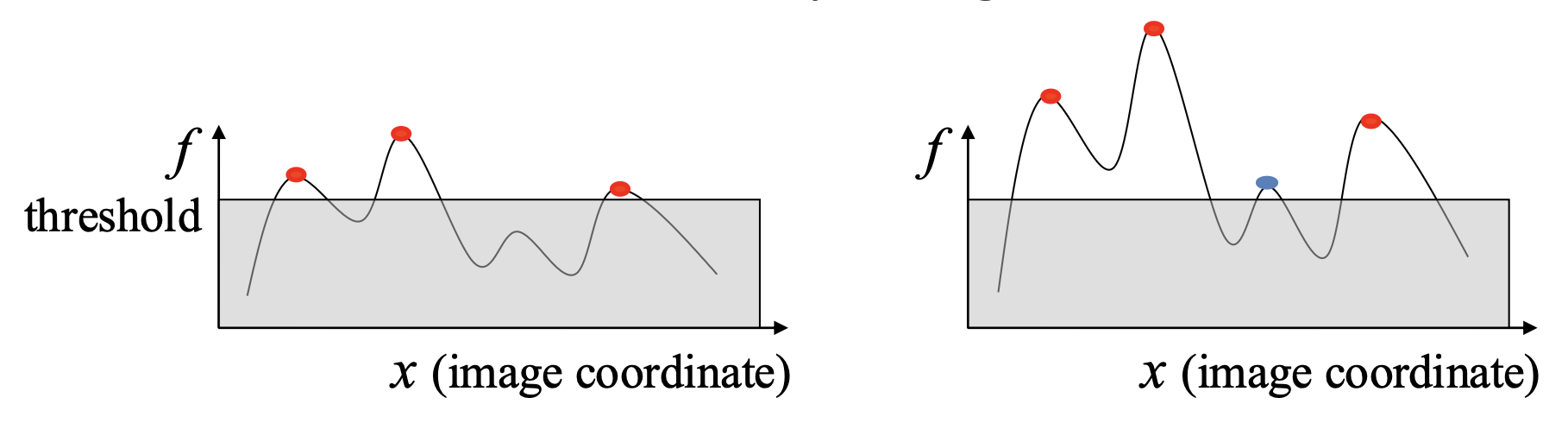
- 为 \(f\) 设置阈值
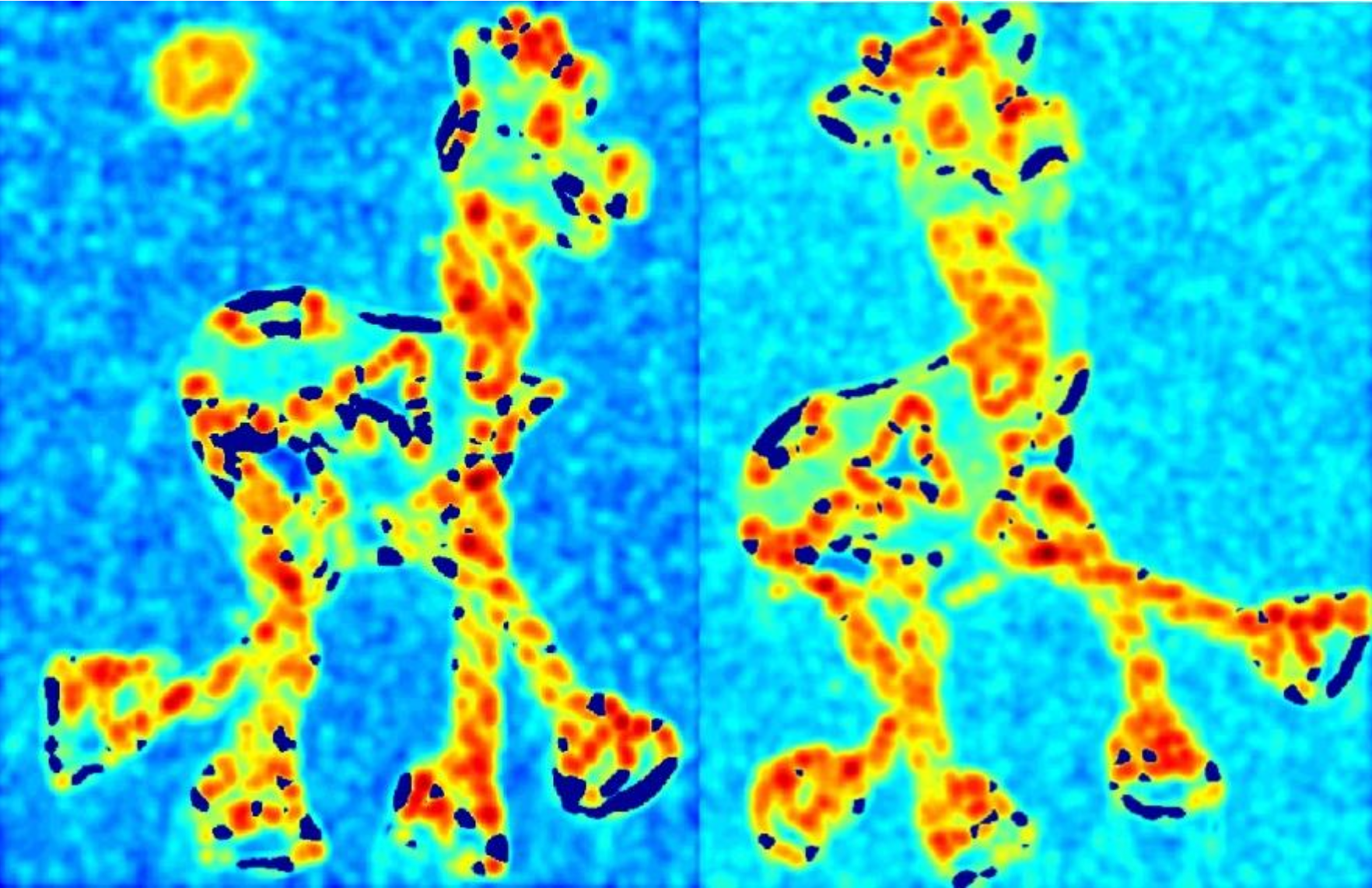
- 寻找响应函数的局部极大值(非极大值抑制 (nonmaximum suppression))
对于上面例子的结果,如何确保这些点是可重复的(repeatable)?如何从数学层面定义这个可重复性?我们希望对应像素上的响应值在图像变换 (image transformation) 的过程中保持不变(invariant)。
Invariance Properties⚓︎
图像变换包括:
-
光学:
-
光强(intensity) 改变
假设原图像光强为 \(I\),改变后的光强为 \(aI + b\)
- 光强移动(\(I \rightarrow I + b\))是不变的 (invariant)
- 光强缩放(\(I \rightarrow aI\))是变化的 (not invariant)
- 综上,角响应值相对光强变化具有部分的不变性
-
-
几何:
-
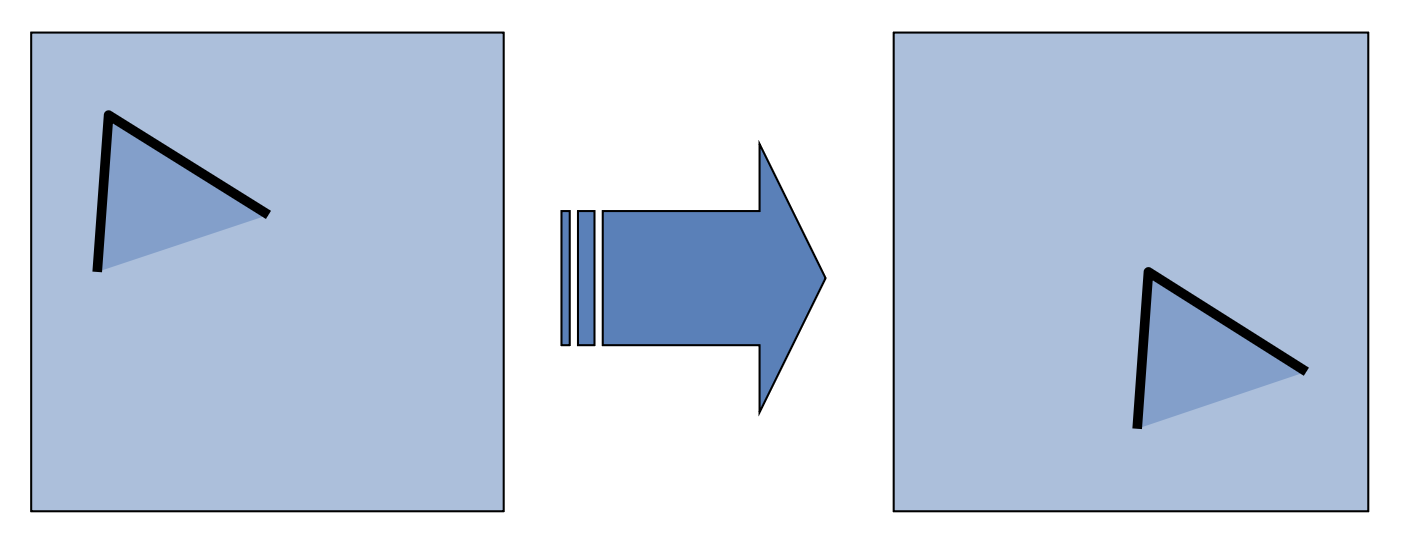
平移(translation):角响应值相对平移具有不变性
-
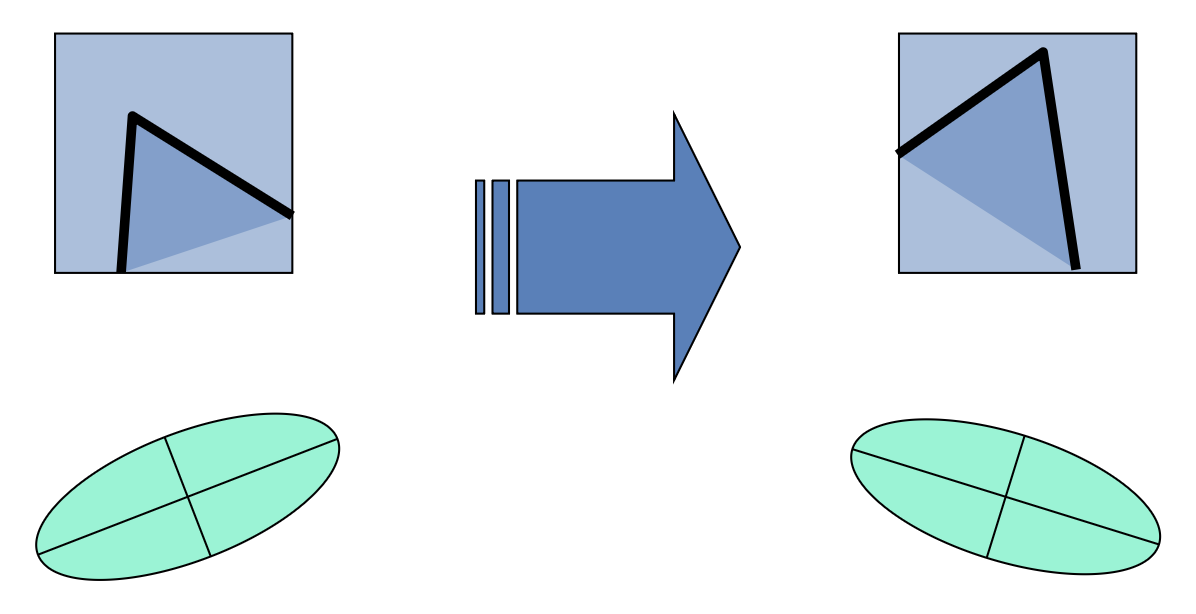
旋转(rotation):角响应值相对旋转具有不变性
-
椭圆旋转,但其形状(即特征值)保持不变
-
-
放缩(scaling):角响应值相对缩放不具有不变性
-
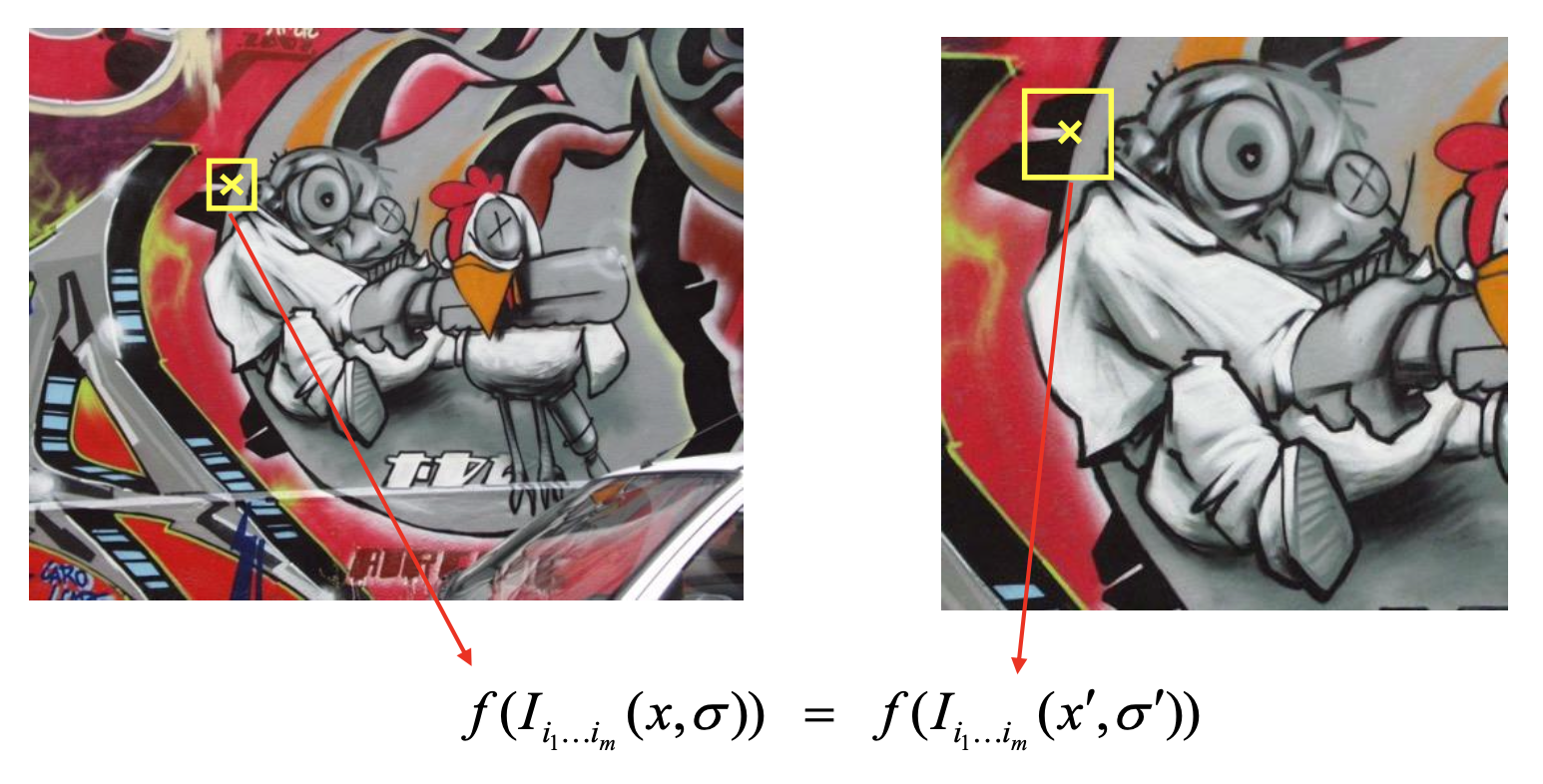
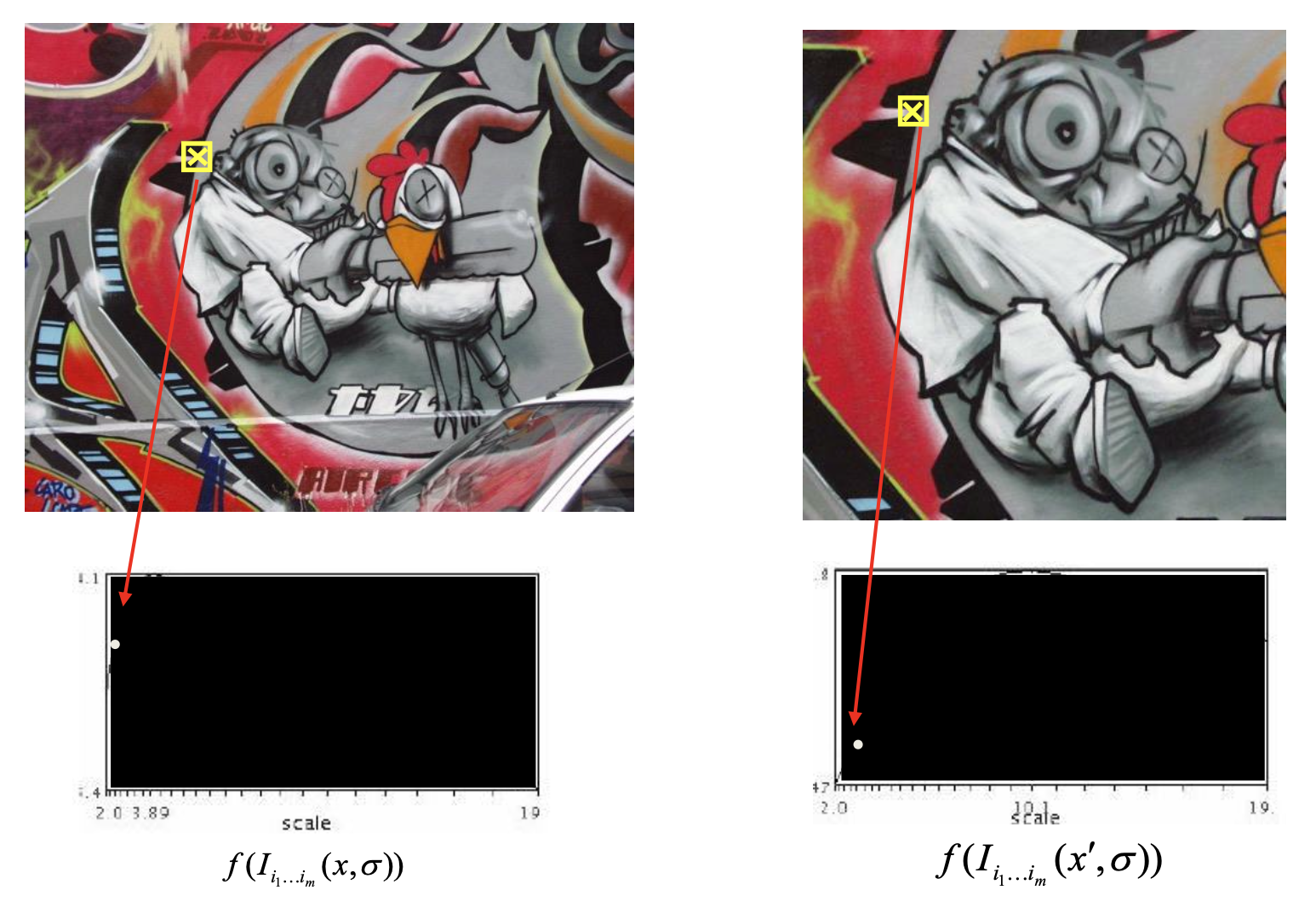
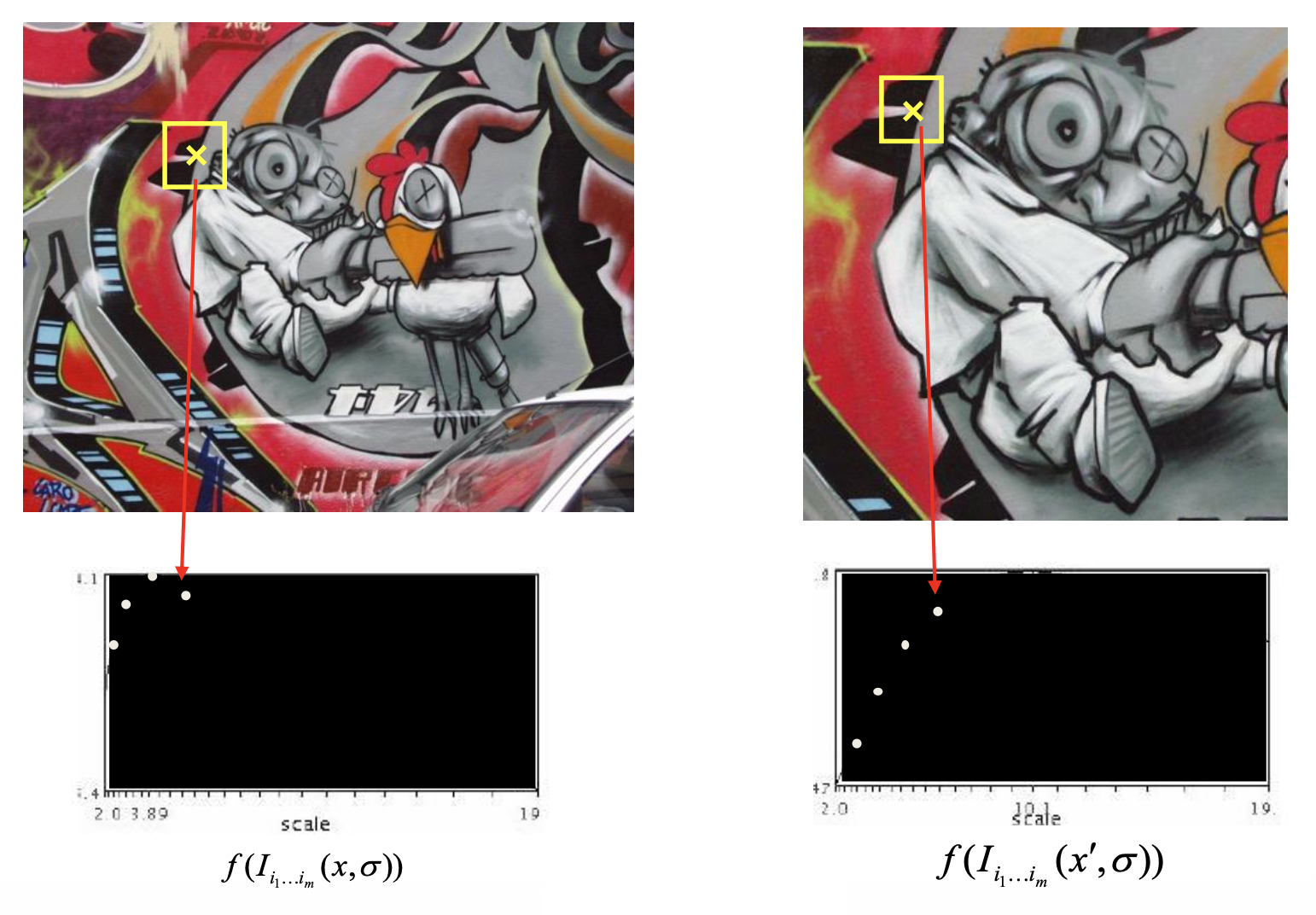
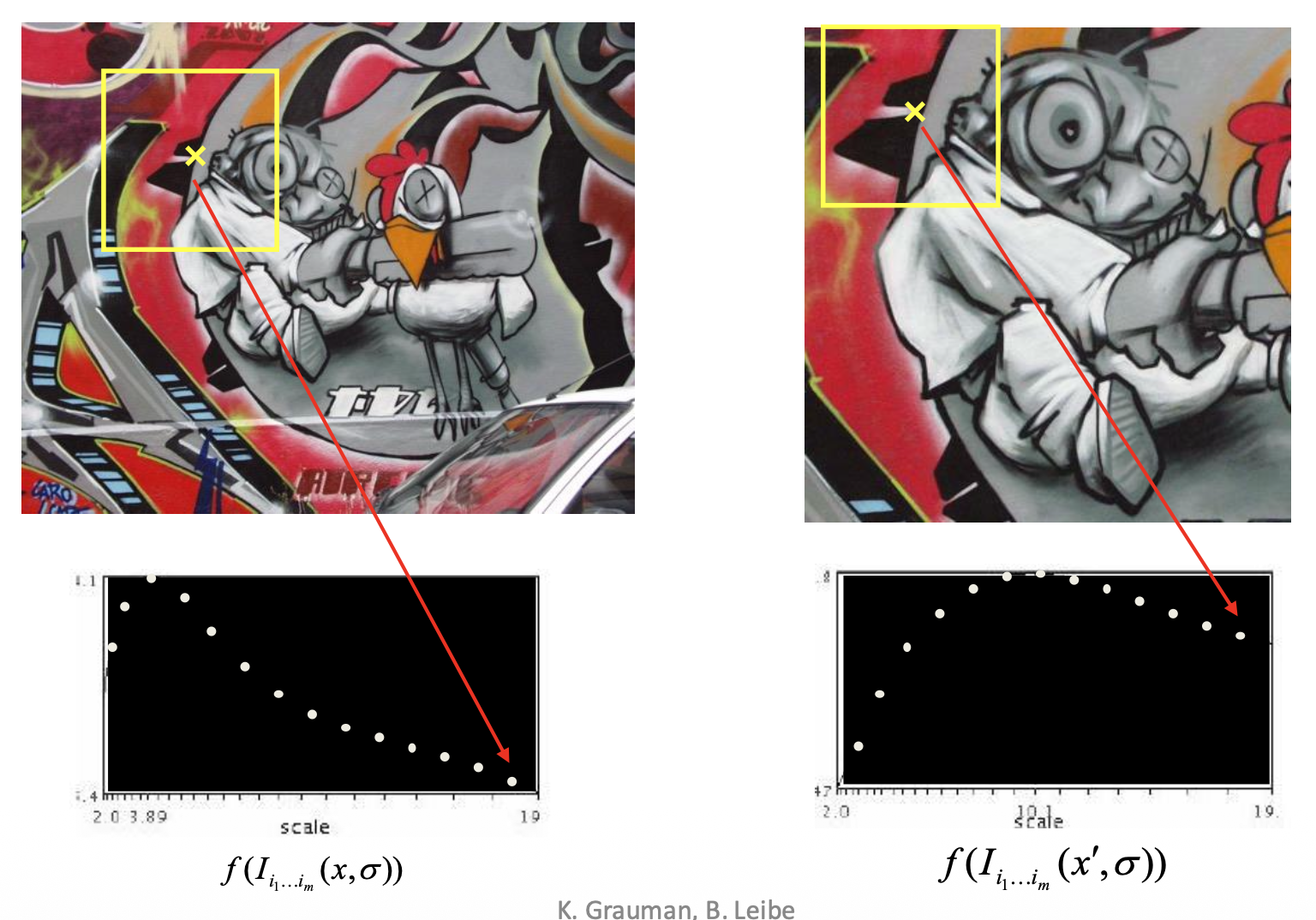
Automatic Scale Selection⚓︎
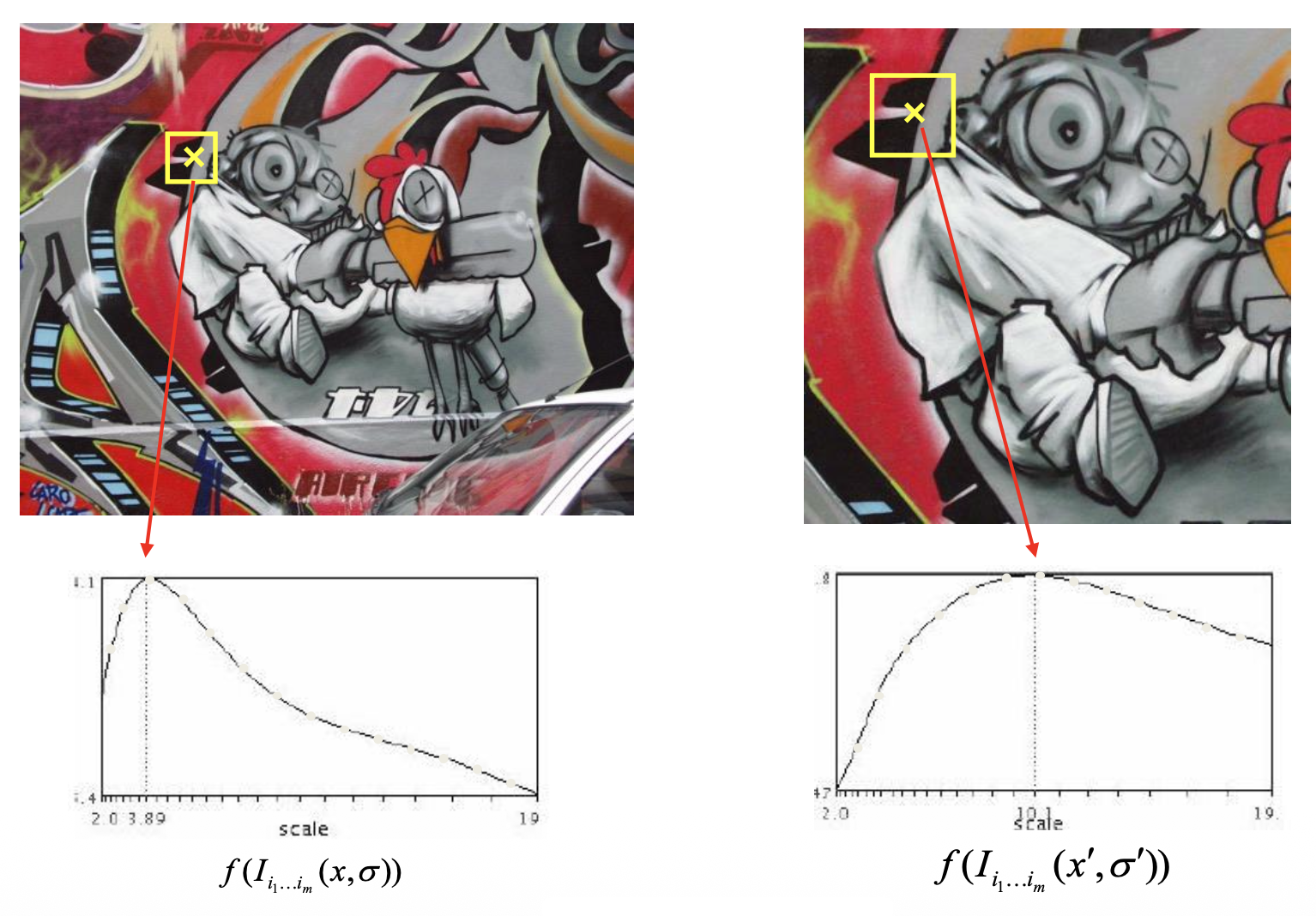
假如要在图像上找角,那么如何确定正确的比例呢?一种解决方案是自动比例选择(automatic scale selection),通过给定的 \(f\) 的局部最大值找出比例:
我们可以采用固定窗口大小,并结合图像金字塔的方法来实现,而不是用越来越大的窗口计算 \(f\)。
Blob Detector⚓︎
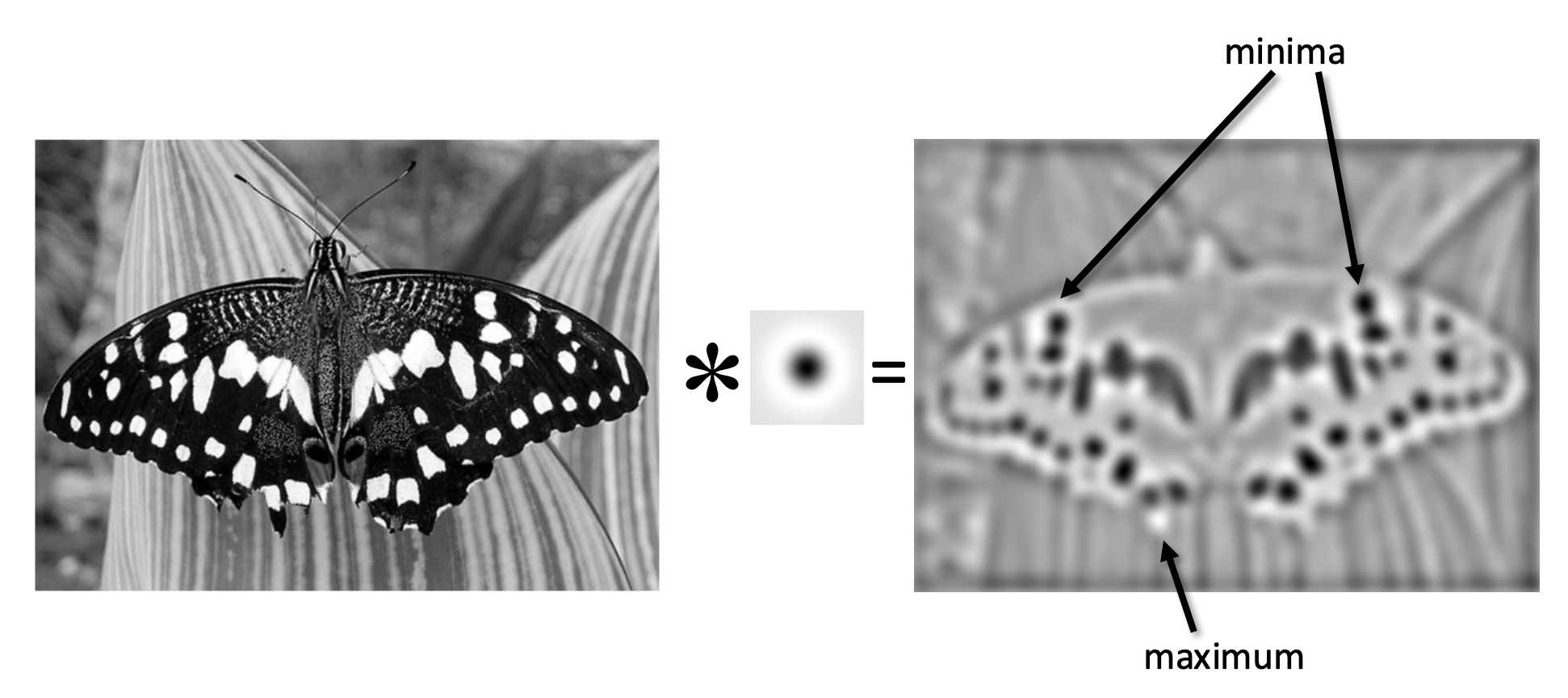
斑点(blob) 是一种不错的图像特征。它在图像光强上有着较大的二阶导数值。因此可通过计算图像的拉普拉斯函数,找到其中的最小值和最大值,从而找到斑点。
接下来的问题是如何计算拉普拉斯呢?
-
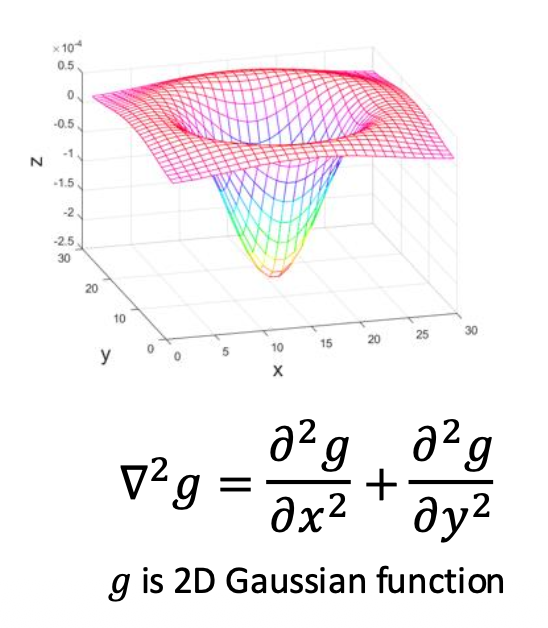
拉普拉斯算子(Laplacian operator)
\[ \nabla^2=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2} \] -
通过滤波计算图像导数
\[ \begin{aligned}&\frac{\partial^{2}f}{\partial x^{2}}=&&f\left(x+1\right)+f\left(x-1\right)-2f\left(x\right)\quad\to\quad\begin{bmatrix}1&-2&1\end{bmatrix} \quad (\text{x kernel}) \\&\frac{\partial^{2}f}{\partial y^{2}}=&&f\left(y+1\right)+f\left(y-1\right)-2f\left(y\right)\quad\to\quad\begin{bmatrix}1\\-2\\1\end{bmatrix} \quad (\text{y kernel})\end{aligned} \] -
拉普拉斯滤波器(Laplacian filter)
由于拉普拉斯滤波器对噪音敏感,因此通常我们会将其和高斯滤波器结合起来一起用,构成了拉普拉斯 - 高斯滤波器(Laplacian of Gaussian, LoG)。
- 先使用高斯滤波器平滑图像
- 然后再计算拉普拉斯值
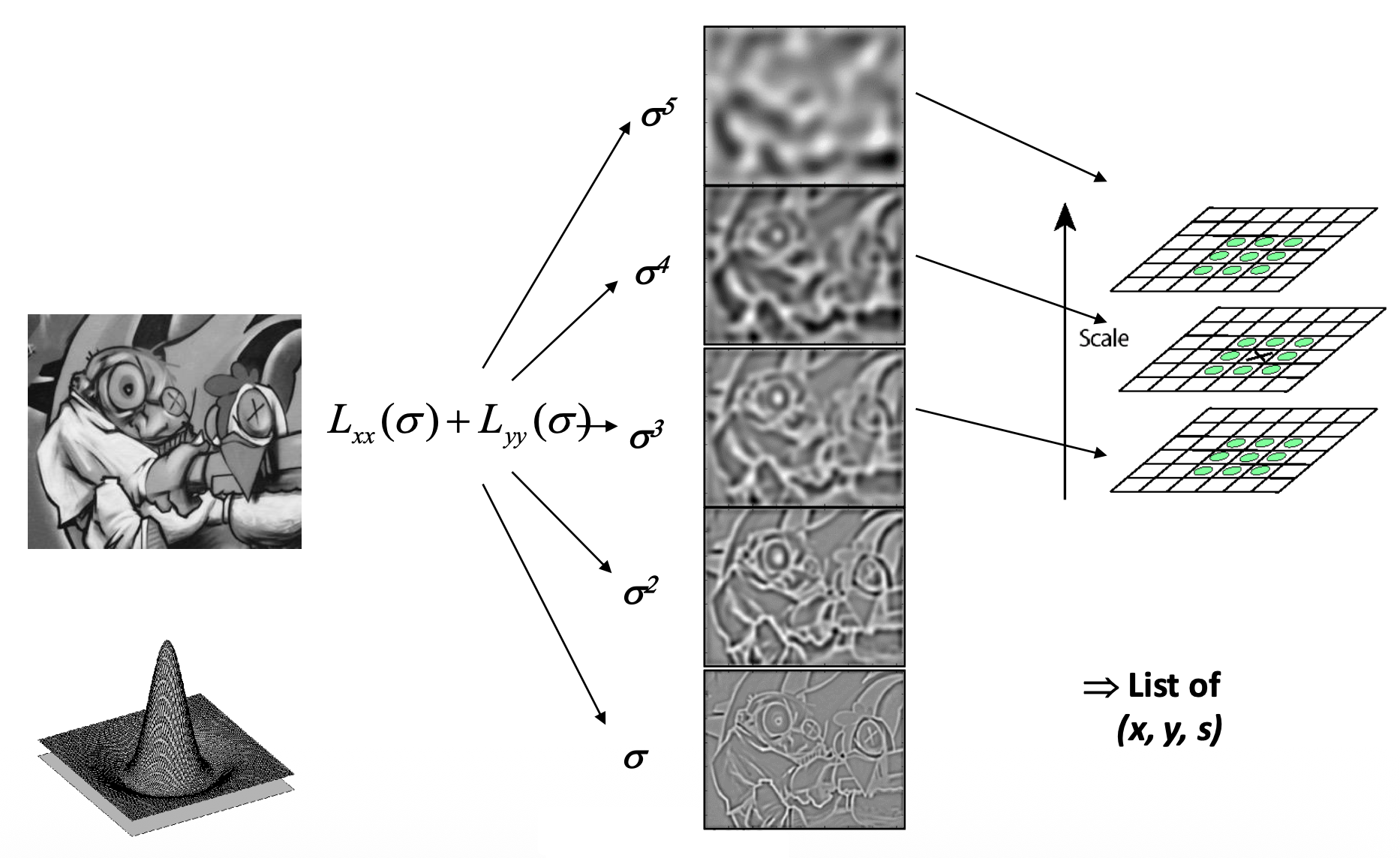
通过以下转换来高效计算 LoG:
- LoG 的比例受高斯函数的 \(\sigma\) 控制
特征点同时是位置和比例的局部最大值:
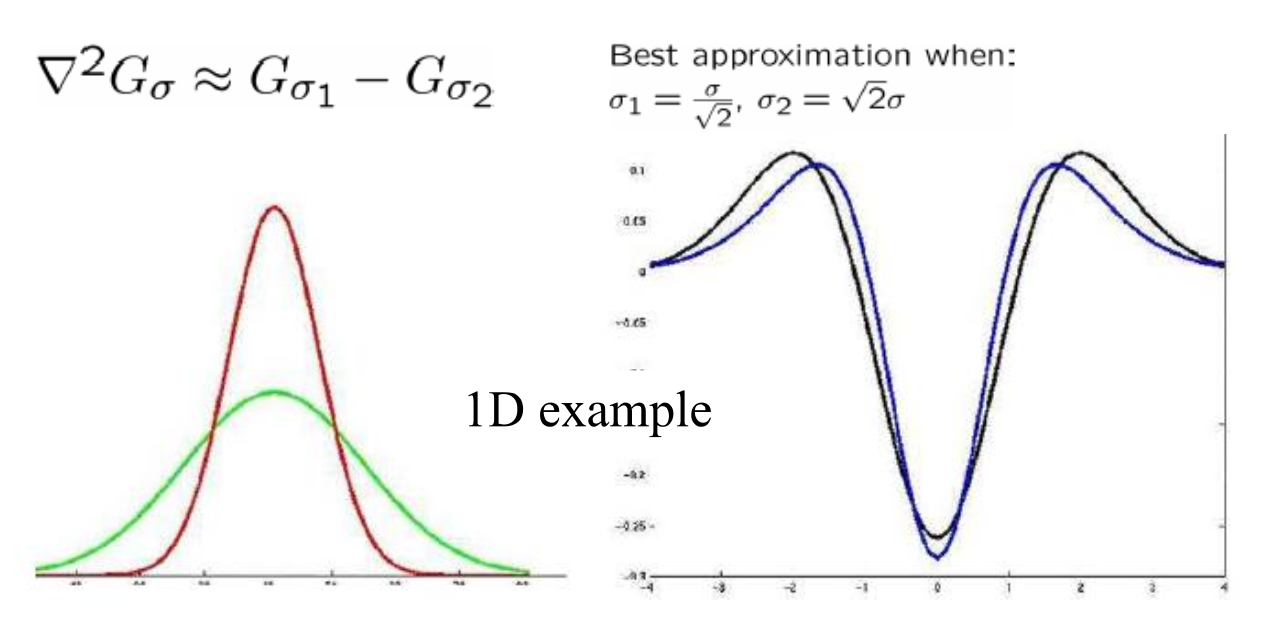
LoG 可用两个高斯函数差(difference of Gaussian, DoG) 近似
使用 DoG 滤波:
- 使用两个高斯滤波器滤波
- 计算两个滤波后图像之差
Description⚓︎
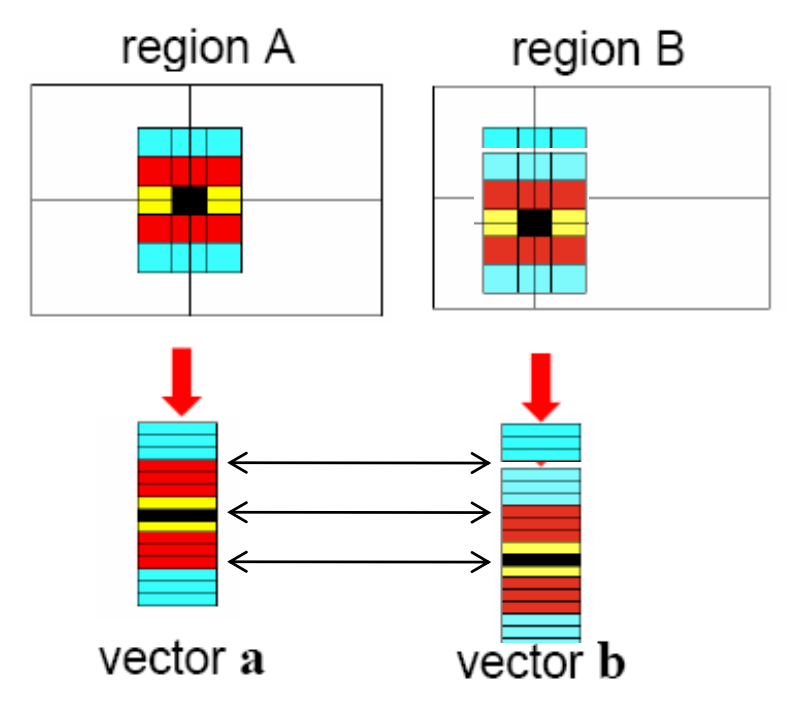
相近内容的图像块 (patch) 应具有相近的描述符 (descriptor)。
描述兴趣点周围区域的最简单方法是记录下光强值列表,从而构成一个特征向量。但这样做的问题是即便对微小的移动或旋转也很敏感(即不是不可变的
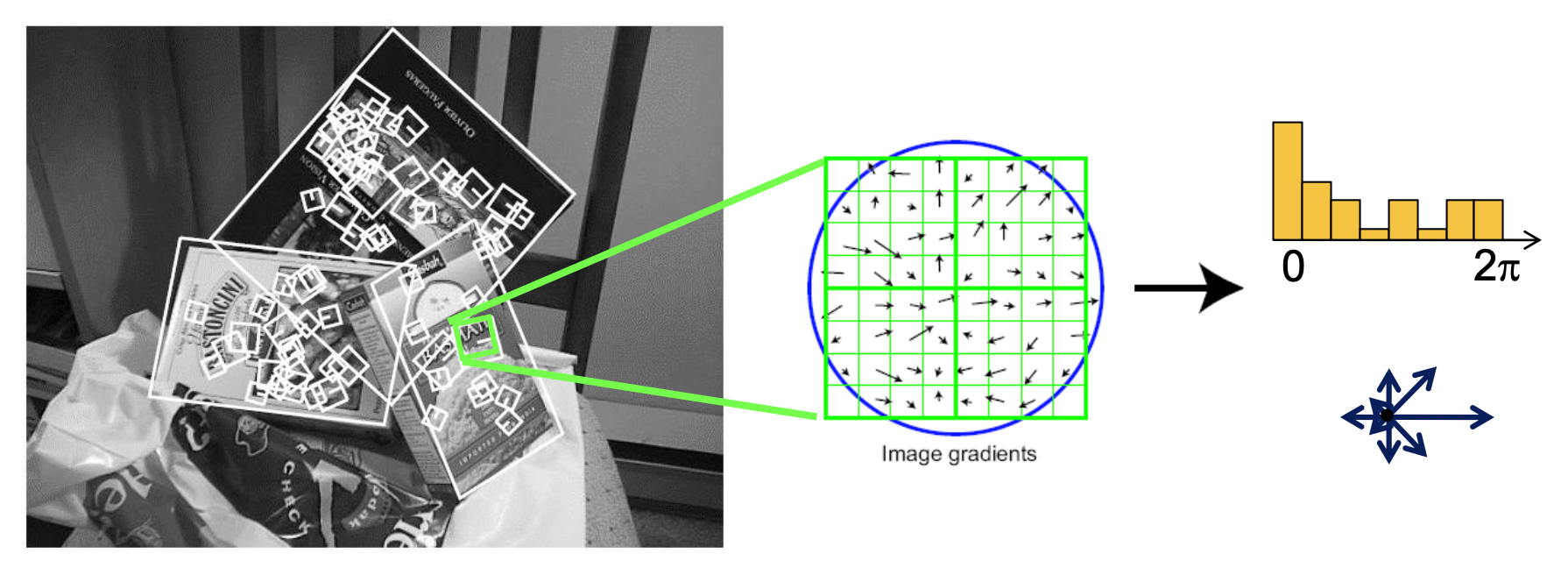
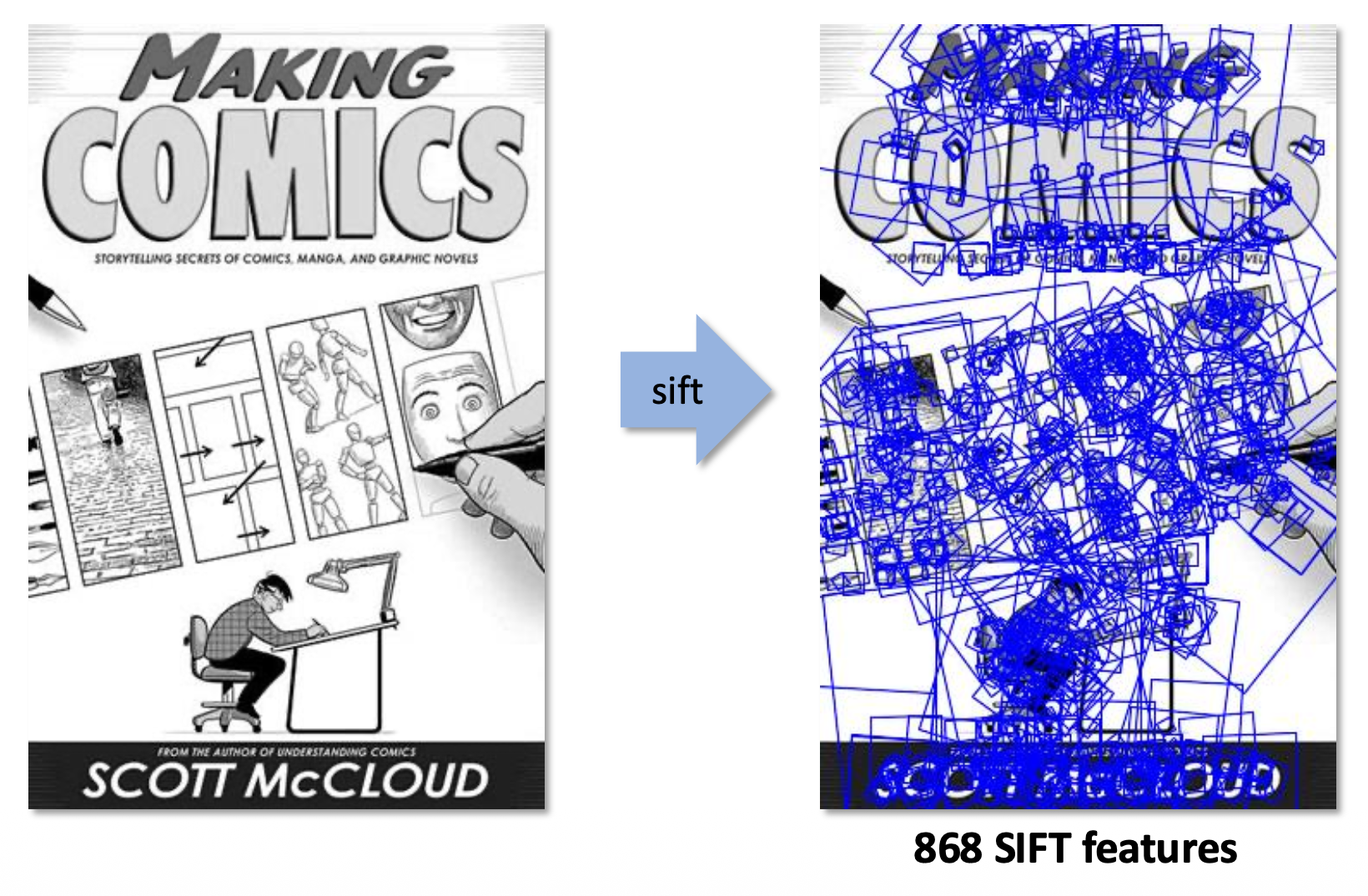
常用的一种方法是 SIFT(尺度不变特征变换 (scale invariant featrue transform))描述符,它有一个关于方向梯度的直方图。
- 捕捉重要的纹理信息
- 对微小平移和仿射形变 (affine deformation) 具有鲁棒性
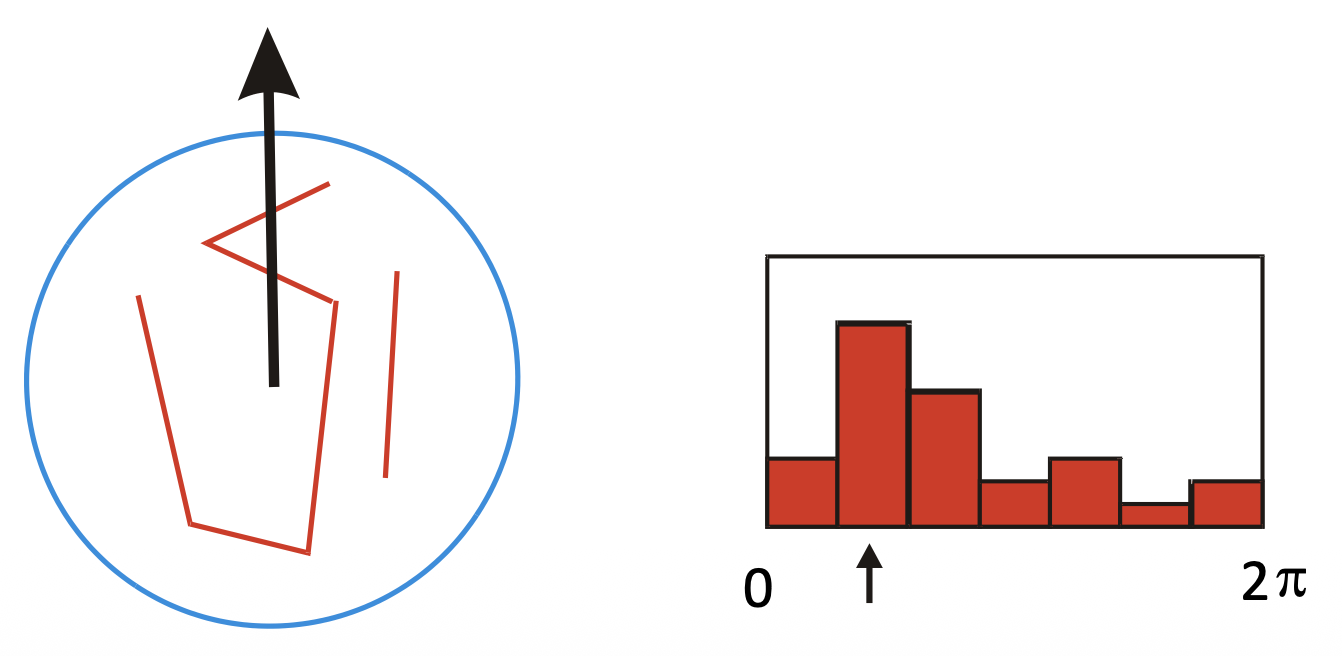
方向归一化(orientation normalization):
- 计算方向直方图
- 选择主方向
- 归一化:旋转至固定方向
Lowe’s SIFT 算法:
- 运行 DoG 检测器(寻找位置 / 尺度空间的最大值)
- 寻找主方向
- 对于每一对(x,y,尺度,方向
) ,创建描述符
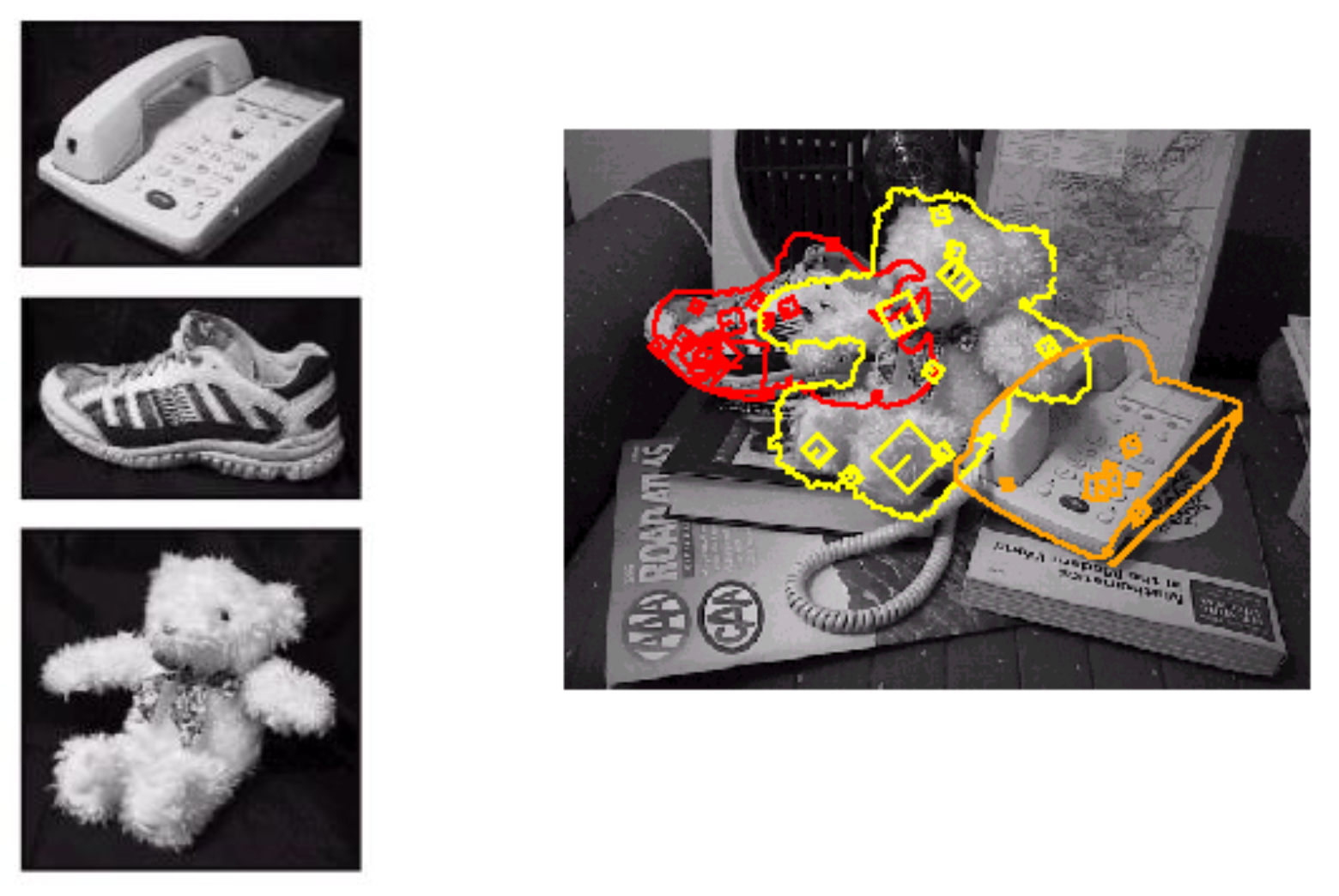
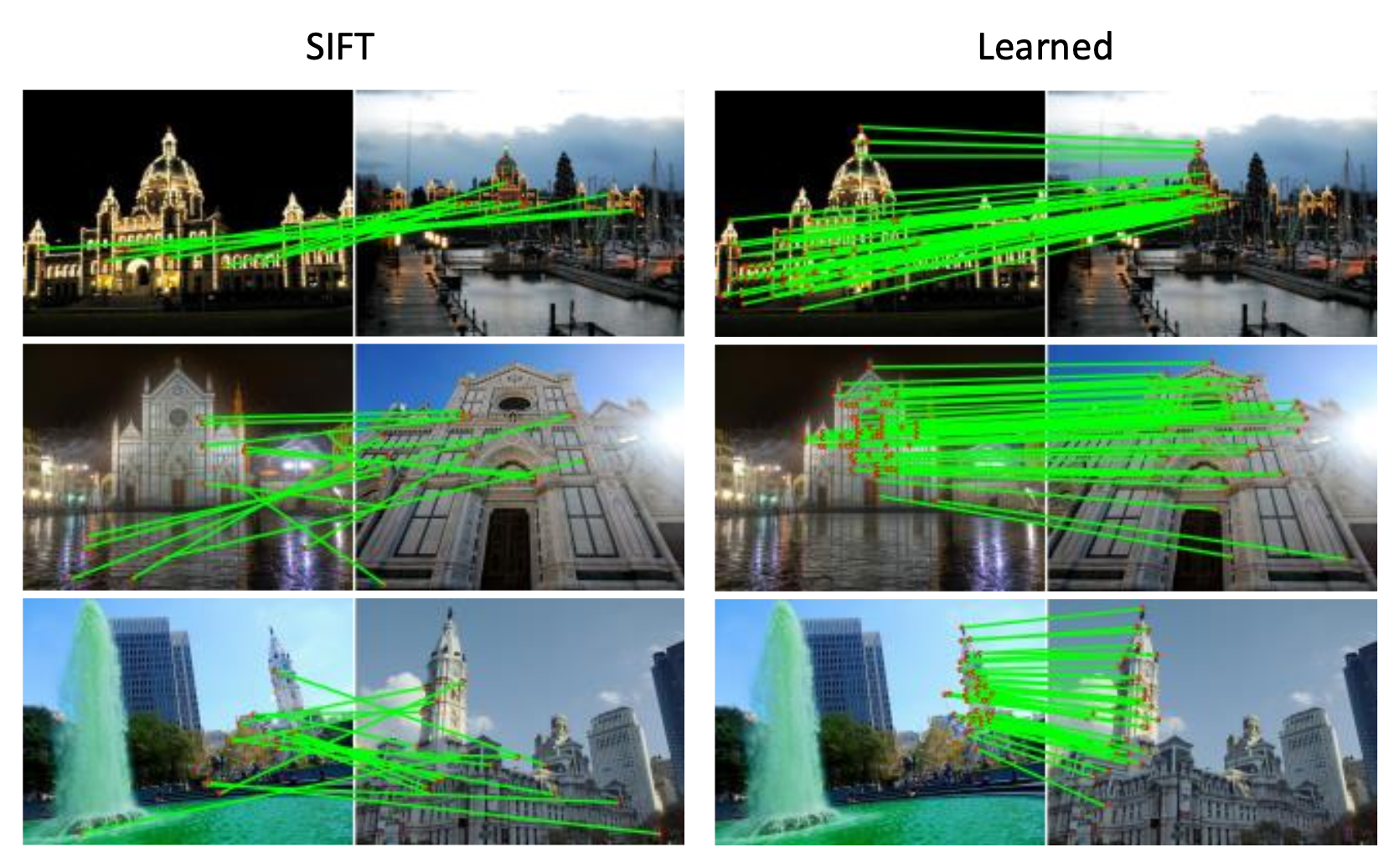
SIFT 的性质——非常鲁棒的匹配技术:
- 能处理视图上的变化,理论上具备对旋转和尺度上的不变性(为什么
? ) - 能处理照明上的巨大变化
- 有时甚至能应对白天 v.s. 夜晚的变化
- 快速且高效,能够实时运行
- 大量可用代码
Matching⚓︎
特征匹配:对于图像 \(I_1\) 的特征,如何找到对应图像 \(I_2\) 上的最佳匹配?
- 定义一个用于比较两个描述符的距离函数
- 测试 \(I_2\) 上的所有特征,找出其中距离最小的那个
这个“距离”的衡量方式有(假设特征为 \(f_1, f_2\)
-
L2 距离 \(\|f_1 - f_2\|\)
- 问题:小距离带来了歧义(不正确)的匹配(比如下图不同位置栅栏部位的匹配)
-
比例测试(ratio test)
-
比例分数 = \(\dfrac{\|f_1 - f_2\|}{\|f_1 - f_2'\|}\),其中
- \(f_2\) 是 \(I_2\) 中对应 \(f_1\) 的最佳匹配
- \(f_2'\) 是 \(I_2\) 中对应 \(f_1\) 的次最佳匹配
-
问题:当比例分数较大时仍然可能带来有歧义的匹配
-
-
相互最近邻居(mutual nearest neighbor)
- \(f_2\) 是 \(I_2\) 中对应 \(f_1\) 的最近邻居
- \(f_1\) 是 \(I_1\) 中对应 \(f_2\) 的最近邻居
Motion Estimation⚓︎
我们生活在运动(motion) 的世界里,因此观察、理解、预测运动是我们日常生活中的重要组成部分。
运动的成因:
-
相机静止,场景移动
-
相机移动,场景静止
-
相机和场景都移动
-
相机静止,场景移动,光源也移动
运动估计存在以下问题:
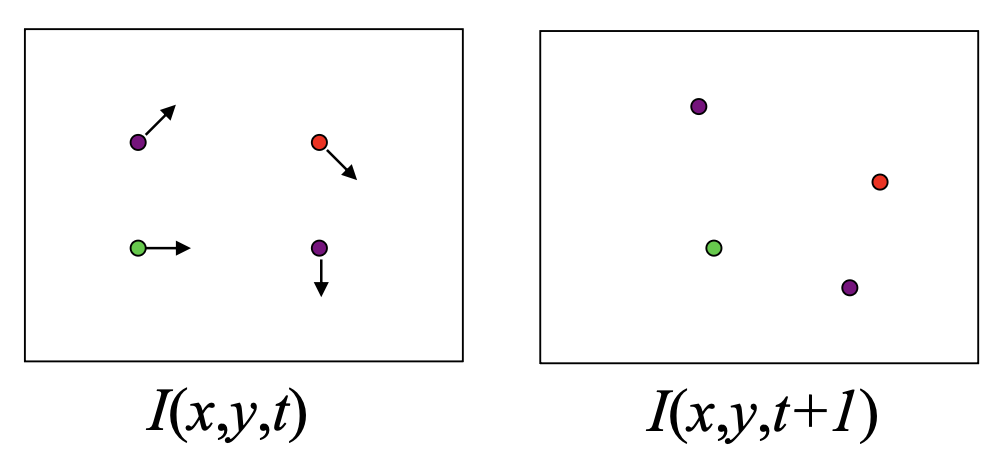
- 特征追踪(feature tracking):提取特征点,并在多帧间追踪它们,输出这些(稀疏)点的位移 (displacement)
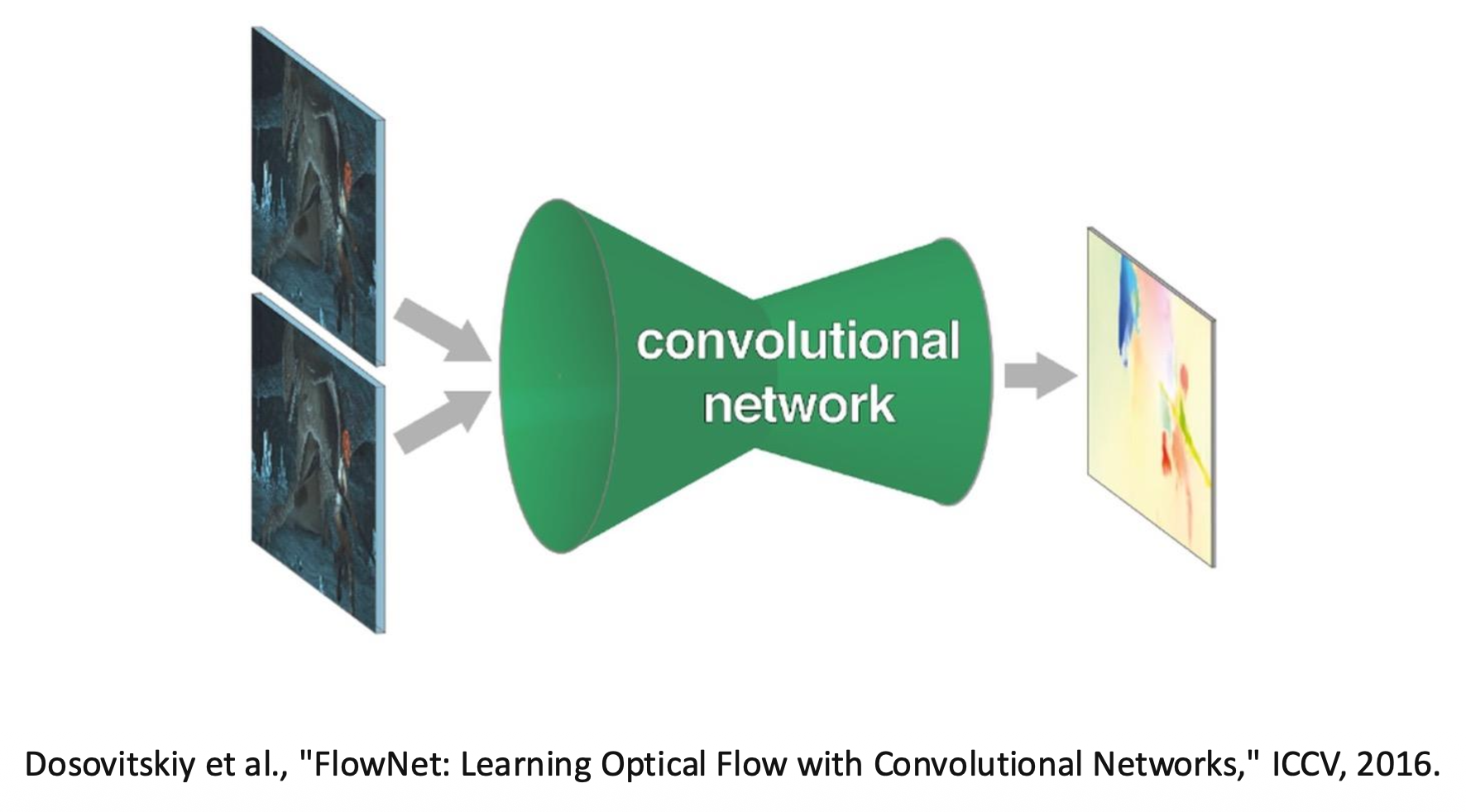
- 光流(optical flow):逐像素还原图像运动,输出密集位移场(光流)
上述两个问题可用一个方法解决,那就是 Lucas-Kanade 法。运用此法时,要先做出以下假设:
-
运动量不大(small motion):点不能移动太远
-
如果移动量太大(比如远超一个像素
) ,那么可以考虑通过降低分辨率的方式来缓减影响
-
-
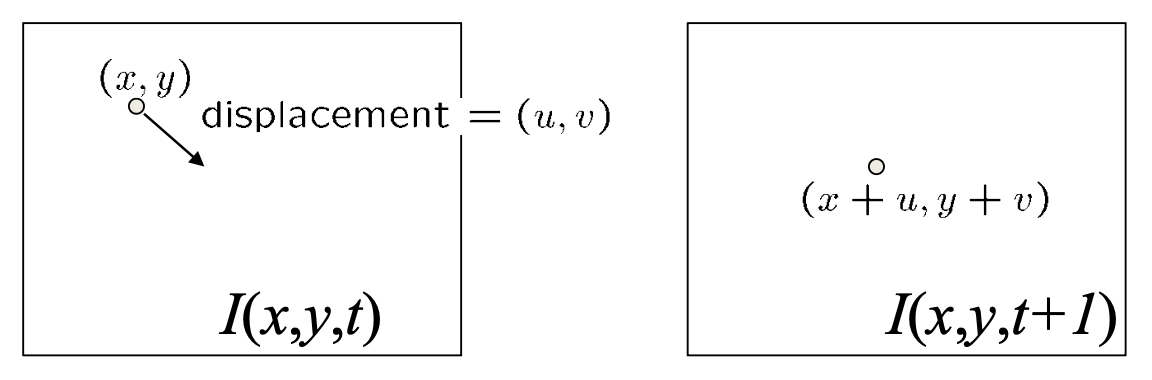
亮度持续性(brightness constancy):相同点在每一帧上看起来应当是相同的
-
亮度持续方程:\(I(x, y, t) = I(x + u, y + v, t + 1)\)
-
由于假设运动量不大,我们可以对方程进行泰勒展开,得到:
\[ \begin{aligned} I(x + u, y + v, t + 1) \approx I(x, y, t) + I_x \cdot u + I_y \cdot v + I_t \\ I(x + u, y + v, t + 1) - I(x, y, t) = I_x \cdot u + I_y \cdot v + I_t \\ I_x \cdot u + I_y \cdot v + I_t \approx 0 \quad \rightarrow \quad \nabla I \cdot \begin{bmatrix}u & v\end{bmatrix}^T + I_t = 0 \end{aligned} \] -
不过目前已知方程只有一个,但有两个未知数 \((u, v)\);要想得到更多方程,请看下一条假设——
-
-
空间一致性(spatial coherence):点的移动应当和它的邻居们一致
- 假设像素的邻居们有相同的 \((u, v)\)
-
如果用 5x5 的窗口,那么每个像素就能得到 25 个方程了
\[ \begin{bmatrix}I_x(\mathbf{p_1}) & I_y(\mathbf{p_1}) \\ I_x(\mathbf{p_2}) & I_y(\mathbf{p_2}) \\ \vdots & \vdots \\ I_x(\mathbf{p_{25}}) & I_y(\mathbf{p_{25}})\end{bmatrix} \begin{bmatrix}u \\ v\end{bmatrix} = -\begin{bmatrix}I_t(\mathbf{p_1}) \\ I_t(\mathbf{p_2}) \\ \vdots \\ I_t(\mathbf{p_{25}})\end{bmatrix} \]简化表示为 \(Ad = b\)。现在方程比变量多了。
-
现在的目标是求解 \(\min\limits_d \|Ad - b\|^2\),即关于 \(d\) 的最小二乘问题。以下方程的解即为最终要求的 \(d\):
\[ \begin{aligned} (A^T A) d & = A^T b \\ \underbrace{\begin{bmatrix}\sum I_x I_x & \sum I_x I_y \\ \sum I_x I_y & \sum I_y I_y\end{bmatrix}}_{A^TA}\begin{bmatrix}u \\ v\end{bmatrix}&=-\underbrace{\begin{bmatrix}\sum I_x I_t \\ \sum I_y I_t\end{bmatrix}}_{A^Tb} \end{aligned} \] -
该方程何时能解:\(A^TA\) 可逆 (invertible) 且是良态的 (well-conditioned)
- 它的特征值 \(\lambda_1, \lambda_2\) 不应过小
- 这和哈里斯角检测器类似
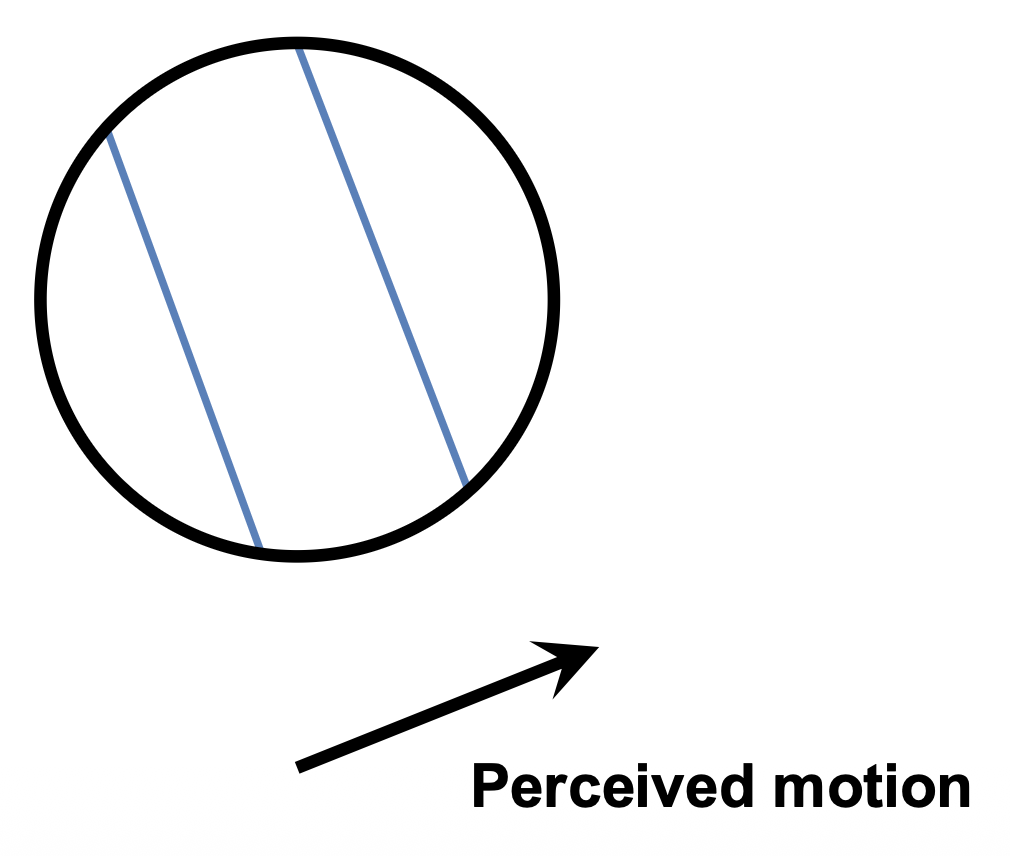
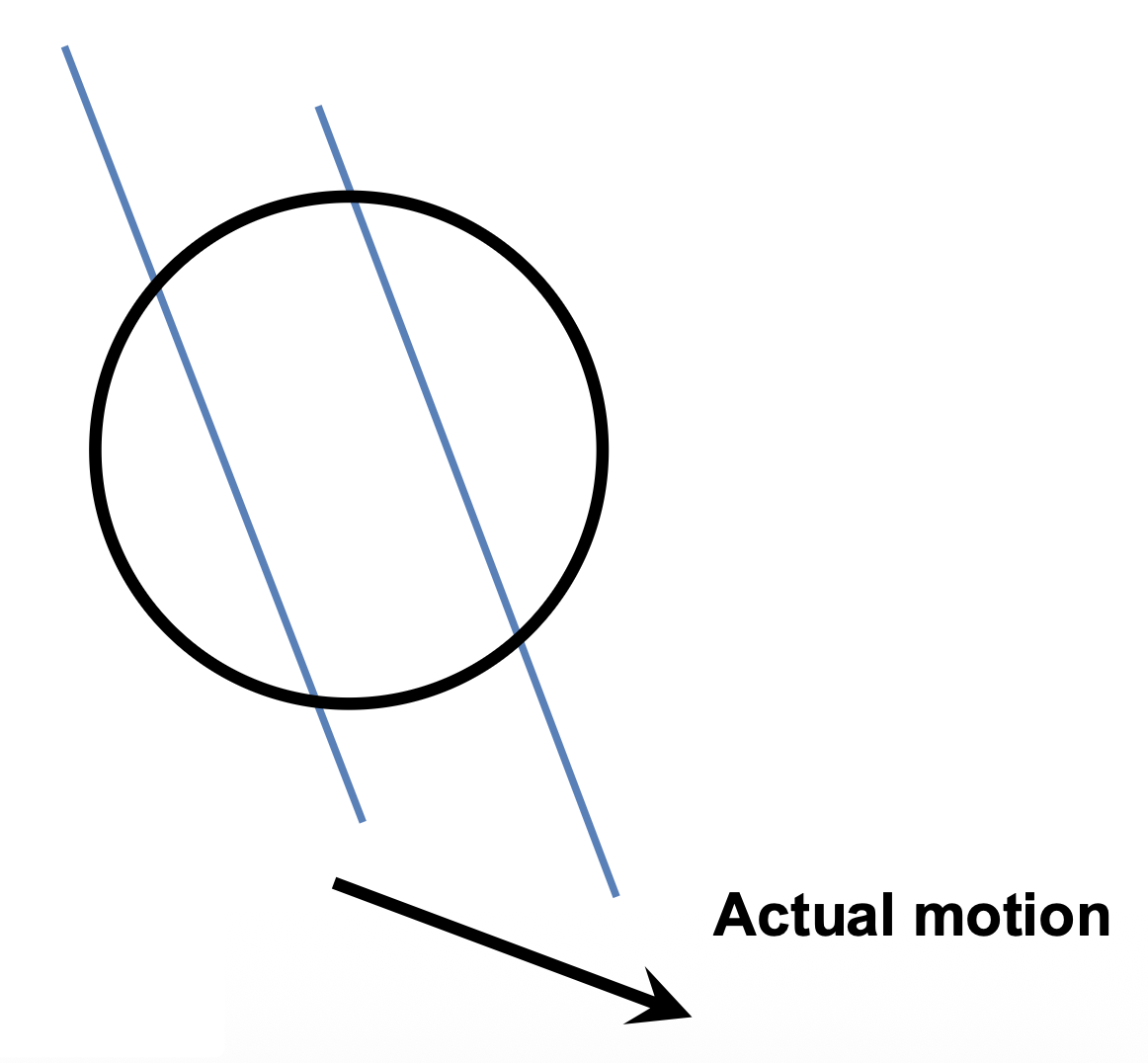
孔径问题(aperture problem):平行于边缘的运动分量无法测量。
导致 Lucas-Kanade 法存在误差的潜在原因有:
- 假设 \(A^TA\) 是容易可逆的
- 假设图像上没有太多噪声
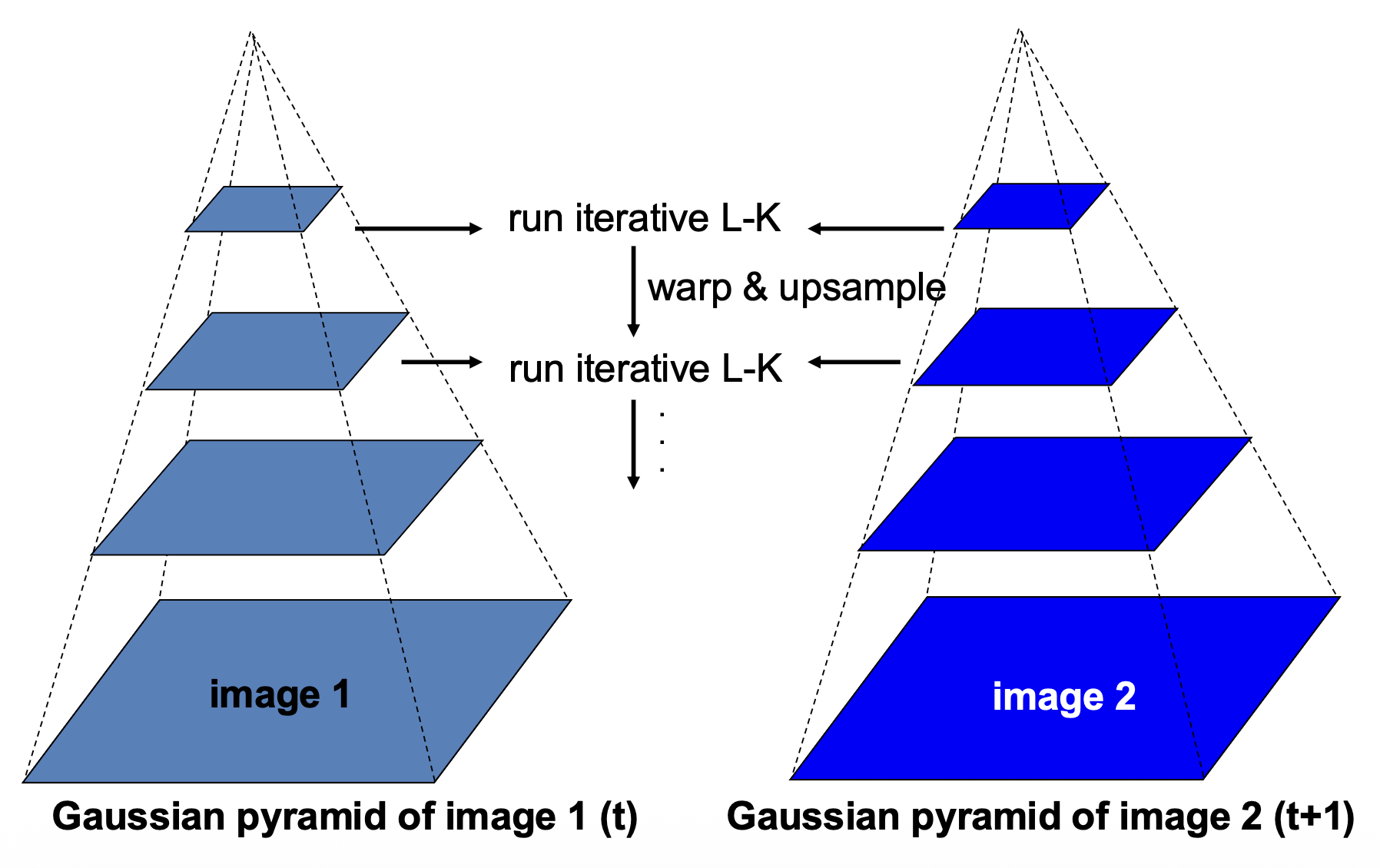
从粗到精的光流估计(coarse-to-fine optical flow estimation):
例子
评论区