Model Fitting and Optimization⚓︎

约 1815 个字 5 行代码预计阅读时间 9 分钟

Optimization⚓︎

例子

例 1 例 2 例 3

\[ \begin{aligned} \text{minimize} \quad & f_0(x) \\ \text{subject to} \quad & f_i(x) \le 0, i = 1, \dots, m \\ & g_i(x) = 0, i = 1, \dots, p \end{aligned} \]

$x \in \mathbb{R}^n$ 是被选中的（向量）变量
$f_0$ 是要被最小化的目标函数
$f_1, \dots, f_m$ 是不等式约束函数
$g_1, \dots, g_p$ 是等式约束函数

图像去模糊

Model Fitting⚓︎

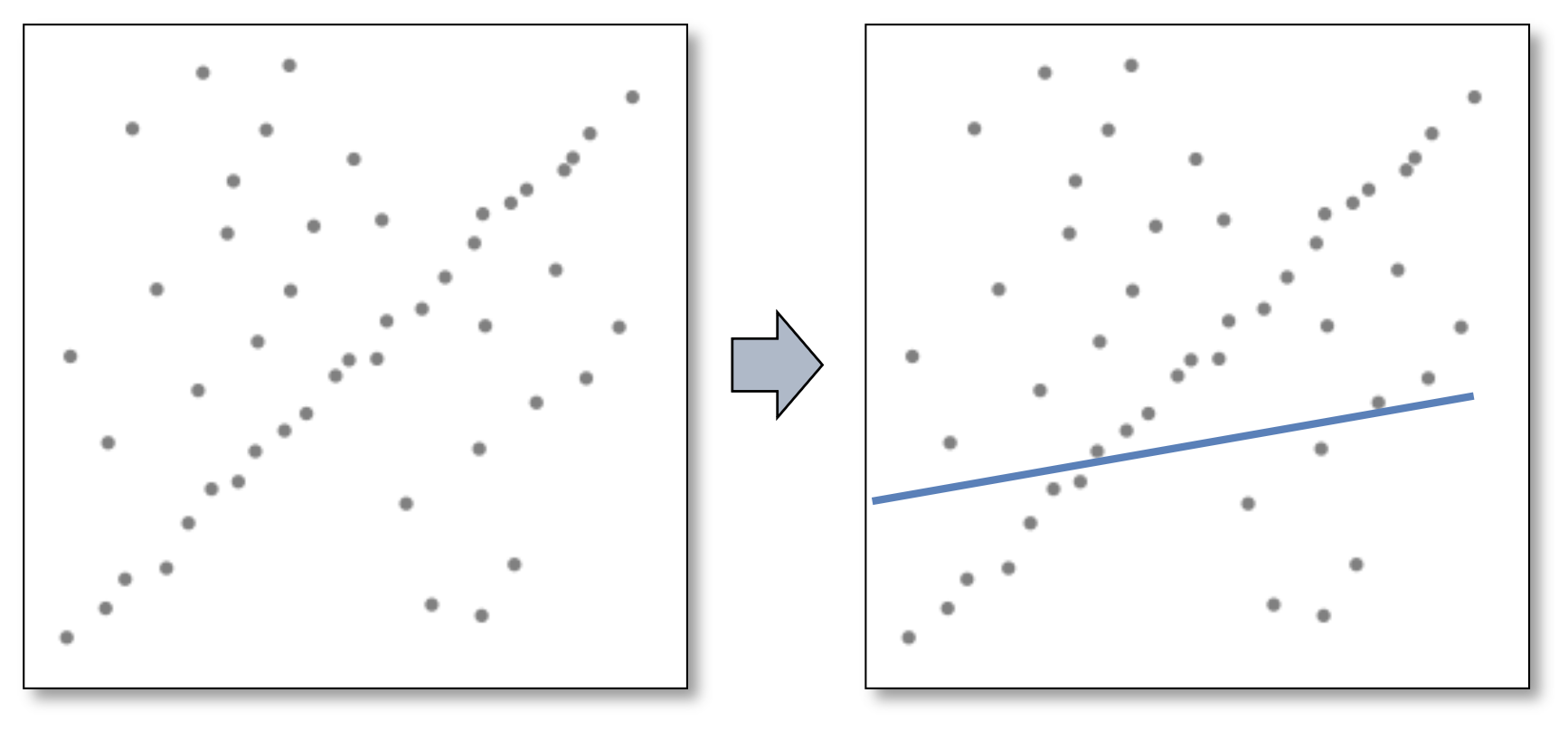
数学模型 $b = f_x(a)$ 描述了输入 $a$ 和输出 $b$ 之间的关系，期中 $x$ 为模型参数。

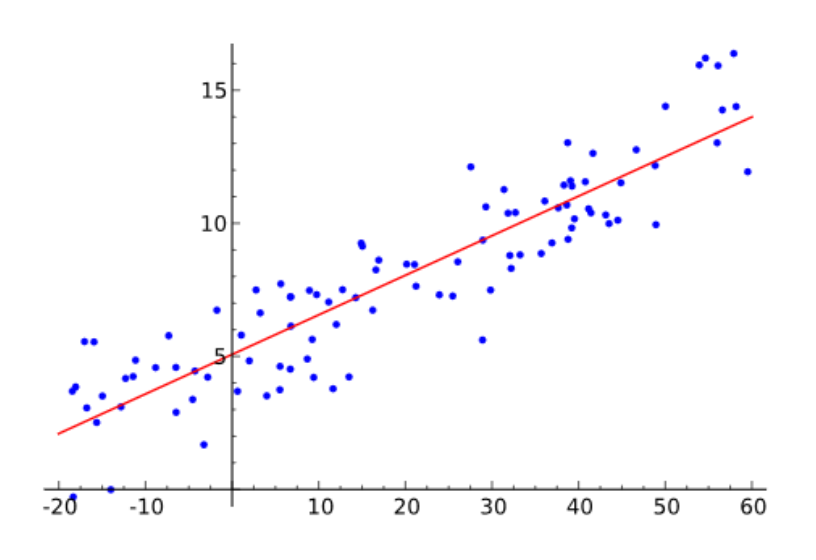
例子：线性模型 $b = a^T x$（如右图所示）

那么如何根据数据估计模型参数（这一过程通常称之为学习(learning)）呢？一种典型的方法是最小化均方差(mean square error, MSE)，即：

\[ \hat{x} = \arg \min\limits_x \sum_i (b_i - a_i^T x)^2 \]

Maximum Likelihood Estimation⚓︎

假设数据带有高斯噪音，即： $$ b_i = a_i^T x + n, n \sim G(0, \sigma) $$

对于给定 $x$，观察到 $(a_i, b_i)$ 的可能性为： $$ P[(a_i, b_i)|x] = P[b_i - a_i^T x] \propto \exp \left(-\dfrac{(b_i - a_i^T x)^2}{2 \sigma^2}\right) $$

如果这些数据点都是独立的，那么：

\[ \begin{aligned} & P[(a_1, b_1)(a_2, b_2)\dots|x] \\ = & \prod_i P[(a_i, b_i)|x] \\ = & \prod_i P[b_i - a_i^T x] \\ \propto & \exp \left(-\dfrac{\sum_i(b_i - a_i^T x)^2}{2 \sigma^2}\right) = \exp \left(-\dfrac{\|Ax - b\|_2^2}{2 \sigma^2}\right) \end{aligned} \]

最大似然估计(maximum likelihood estimation, MLE) = 最大化找到最佳 $x$ 的可能性，即：

\[ \begin{aligned} \hat{x} & = \arg \max\limits_x P[(a_1, b_1)(a_2, b_2)\dots | x] \\ & = \arg \max\limits_x \exp \left(-\dfrac{\|Ax - b\|_2^2}{2 \sigma^2}\right) \\ & = \arg \min\limits_x \|Ax - b\|_2^2 \end{aligned} \]

所以 MSE 就是带有高斯噪音假设的 MLE。

Numerical Methods⚓︎

一些问题是有分析解(analytical solution) 的，比如对于线性 MSE（$\hat{x} = \arg \min\limits_x \|Ax - b\|_2^2$），$\hat{x}$ 的解可通过以下方程得出： $$ A^T Ax = A^T b $$

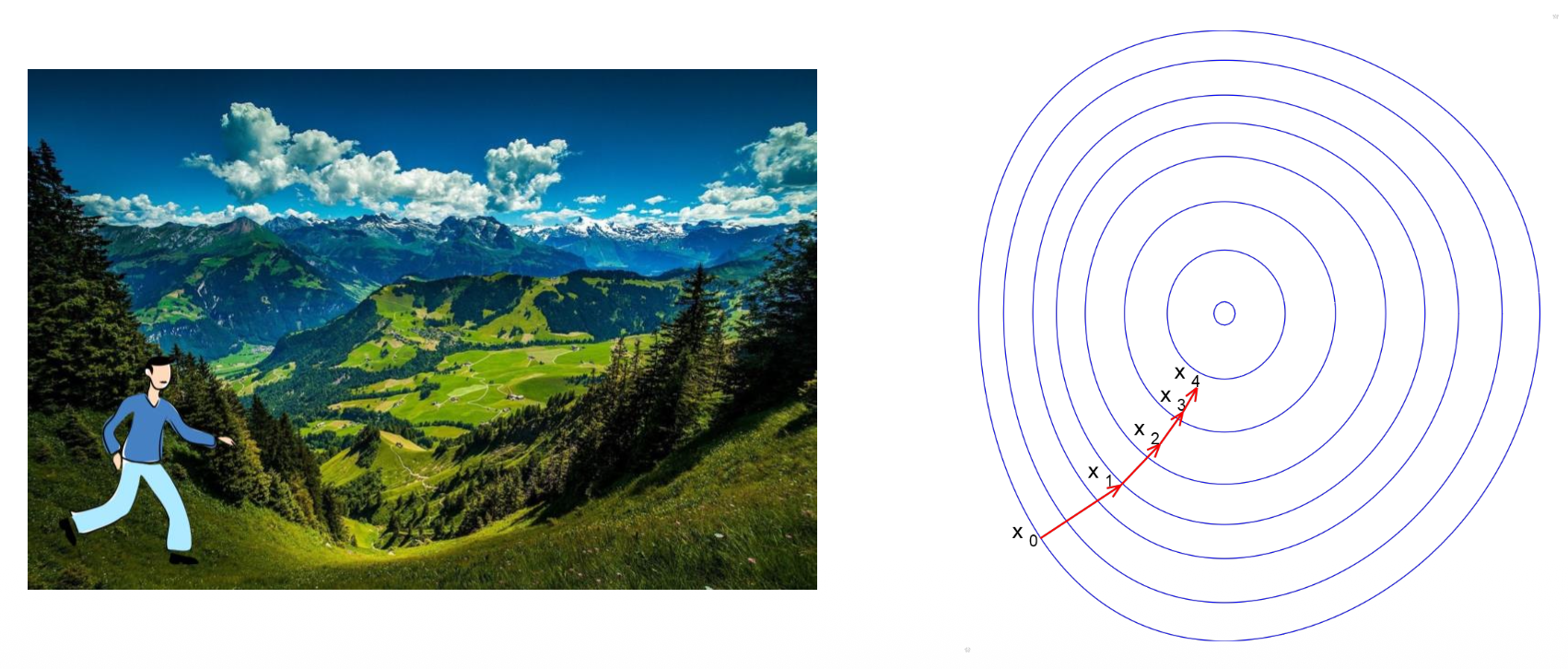
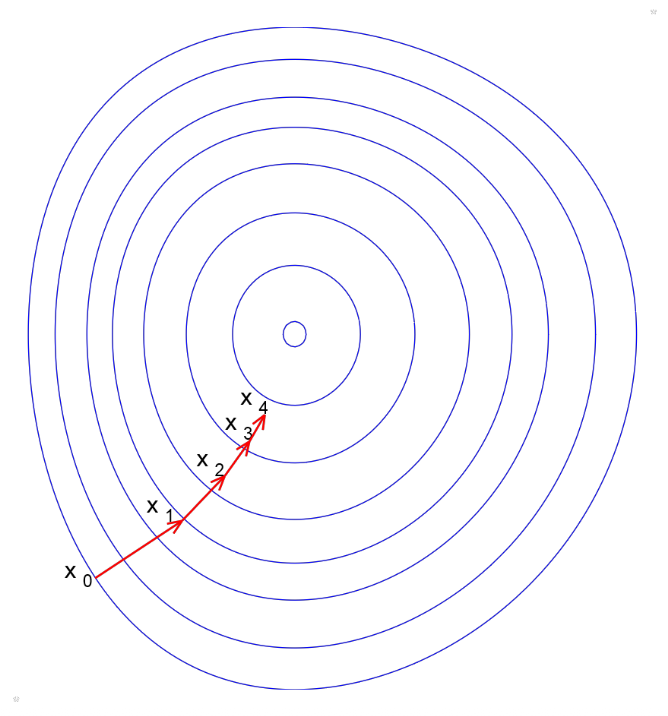
但有些问题没有分析解，比如寻找满足以下条件的路径：$F(x_0) > F(x_1) > \dots > F(x_k) > \dots$。

对于这类问题，我们给出以下算法求解：

x <- x_0  # initialization
while not converge
    h <- descending_direction(x)    # determine the direction
    alpha <- descending_step(x, h)  # determine the step
    x <- x + alpha * x              # update the parameters

现在的问题就变成了如何寻找最佳的 $\bm{h}, \alpha$ 了。

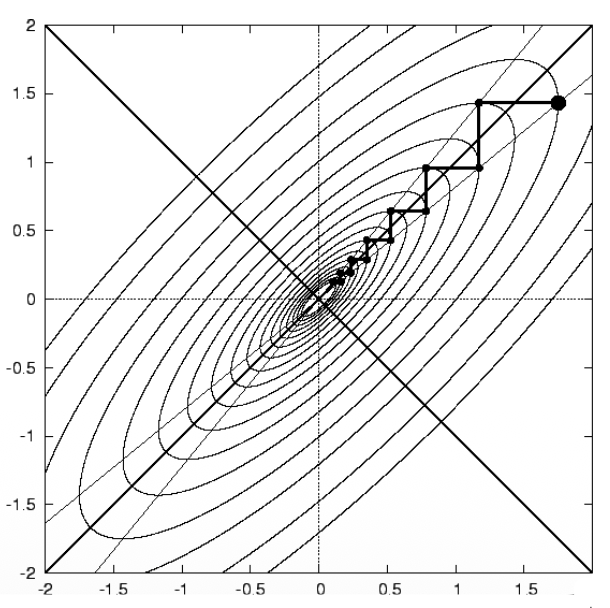
Steepest Descend Method⚓︎

泰勒展开

一阶近似

\[ F(x_k + \Delta x) \approx F(x_k) + J_F \Delta x \]

其中 $\mathbf{J} = \begin{bmatrix}\dfrac{\partial \mathbf{f}}{\partial x_1} \dots \dfrac{\partial \mathbf{f}}{\partial x_n}\end{bmatrix}$ 为雅可比矩阵(Jacobian matrix)（一阶导数）
二阶近似

\[ \begin{aligned}F(x_k+\Delta x)\approx F(x_k)+J_F\Delta x+\frac{1}{2}\Delta x^TH_F\Delta x\end{aligned} \]

其中 $\mathbf{H}=\begin{bmatrix}\frac{\partial^2f}{\partial x_1^2}&\frac{\partial^2f}{\partial x_1\partial x_2}&\cdots&\frac{\partial^2f}{\partial x_1\partial x_n}\\\\\frac{\partial^2f}{\partial x_2\partial x_1}&\frac{\partial^2f}{\partial x_2^2}&\cdots&\frac{\partial^2f}{\partial x_2\partial x_n}\\\\\vdots&\vdots&\ddots&\vdots\\\\\frac{\partial^2f}{\partial x_n\partial x_1}&\frac{\partial^2f}{\partial x_n\partial x_2}&\cdots&\frac{\partial^2f}{\partial x_n^2}\end{bmatrix}$ 为黑塞矩阵(Hessian matrix)（二阶导数）

第一种方法是梯度下降(gradient descent)，它就是通过泰勒展开的一阶近似来确定方向的。

在 $x_0$ 处的泰勒展开

\[ F(x_{0}+\Delta x)\approx F(x_{0})+J_{F}\Delta x \]
当 $J_F \Delta x < 0$ 时，目标函数就会下降
- 当 $\Delta x$ 的方向和 $-J_F^T$ 一样时，目标函数下降幅度最大（即最陡(steepest)）

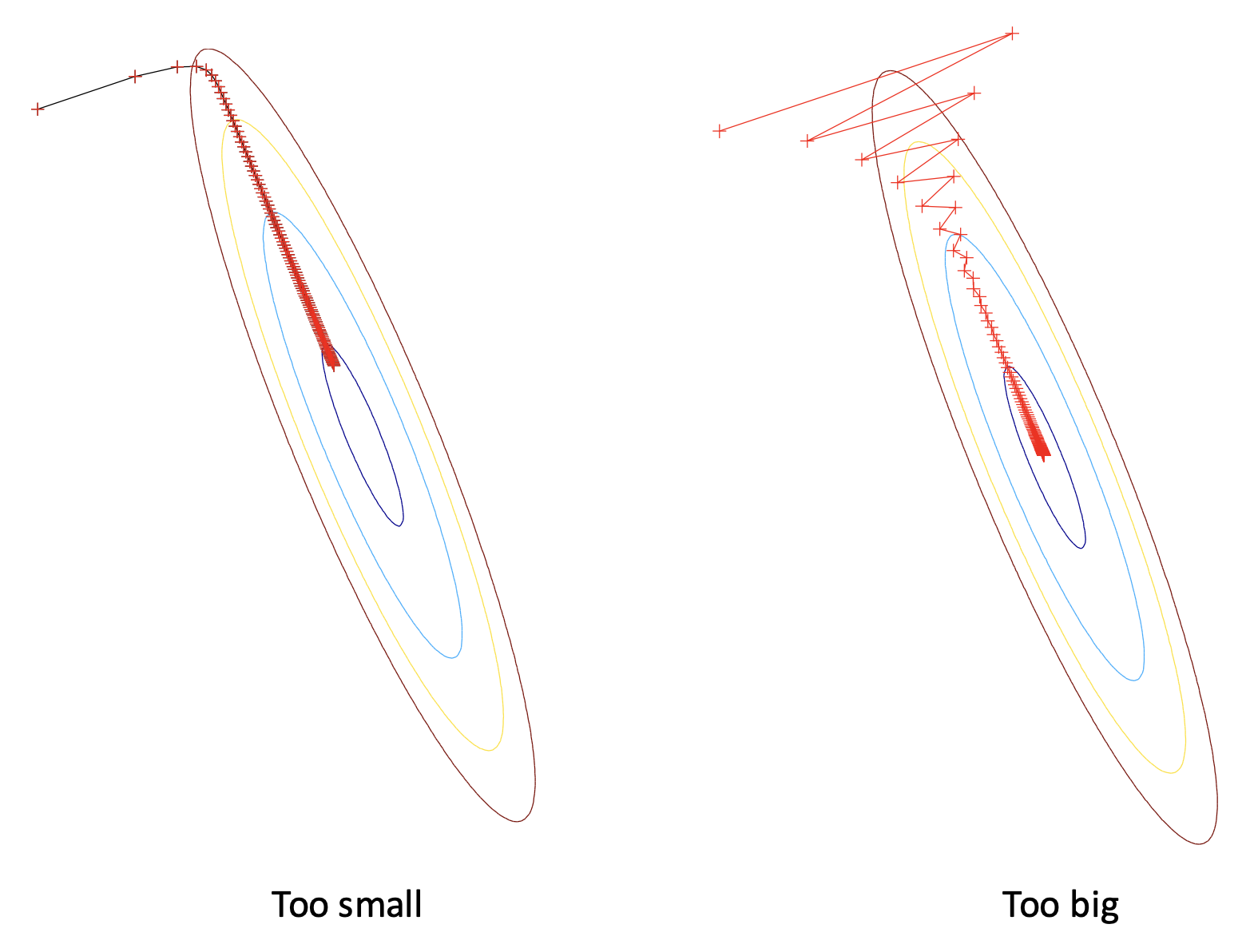
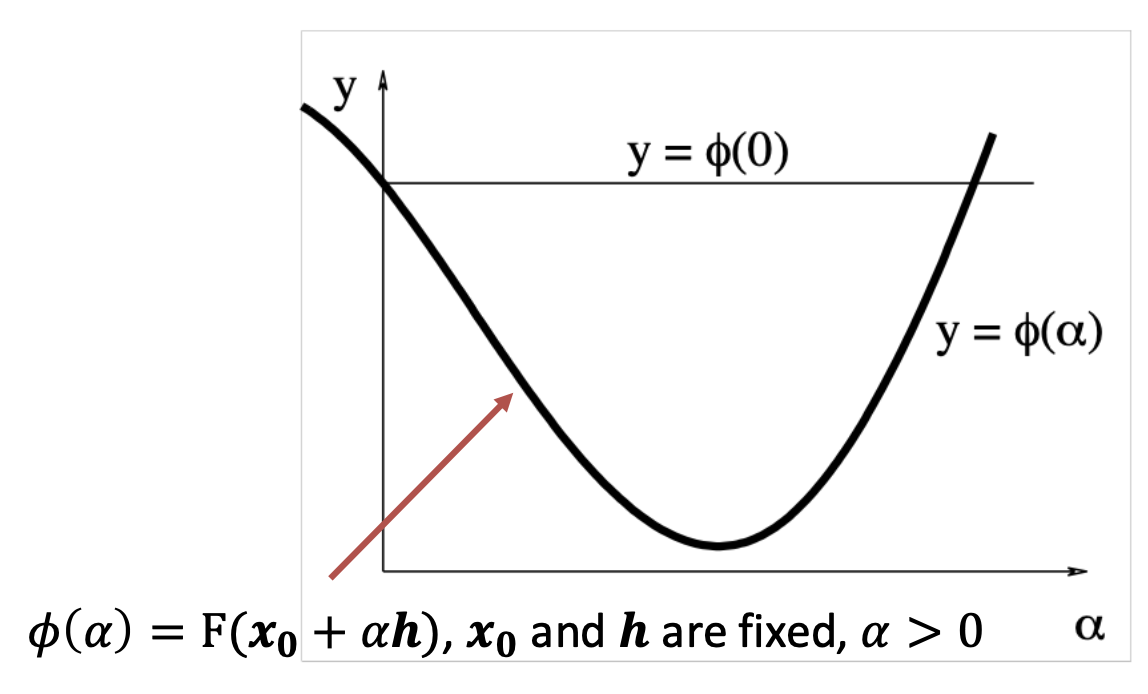
步长(step size) 的影响：

确定步长：

$\alpha$ 太小，$\varphi(\alpha)$ 的改变也很小 -> 增大 $\alpha$
$\alpha$ 太大，$\varphi(\alpha) > \varphi(0)$ -> 减小 $\alpha$
$\alpha$ 和 $\varphi(\alpha)$ 接近 -> 可接受的

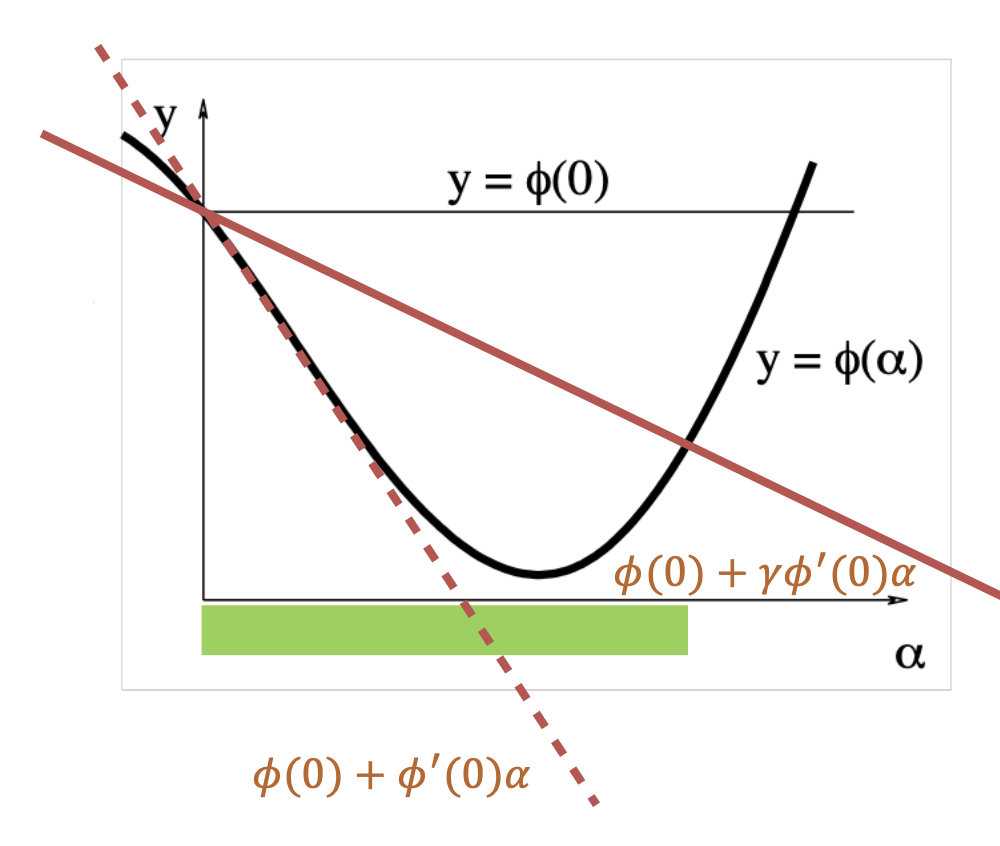
精确的直线搜索
回溯算法(backtracking algorithm)
- 使用一个很大的 $\alpha$ 值初始化
- 减小 $\alpha$，直到 $\phi(\alpha)\leq\phi(0)+\gamma\phi^{\prime}(0)\alpha$
  - 其中参数 $0 < \gamma < 1$

最陡下降法

优点
- 易于实现
- 在远离最小值时表现不错
缺点
- 接近最小值时收敛很慢
  - 原因：只使用一阶导数，没用到曲率
- 浪费大量计算

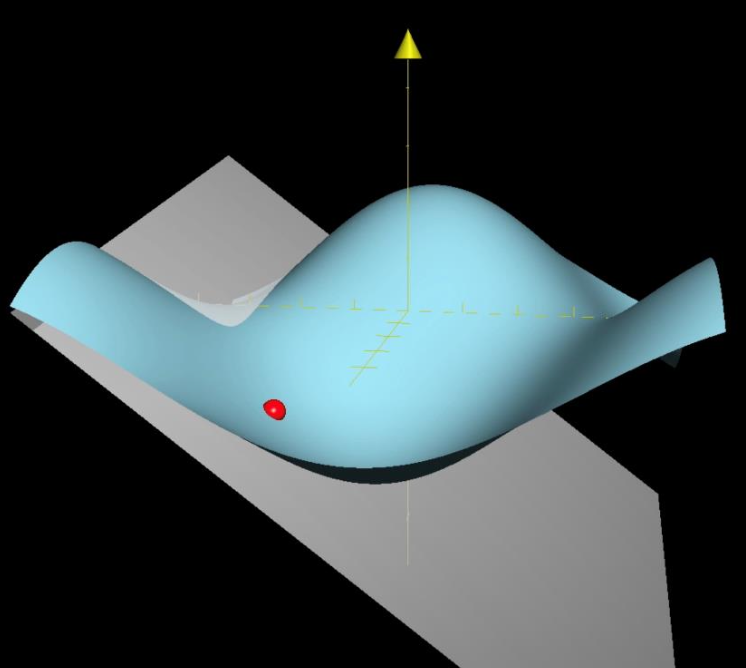
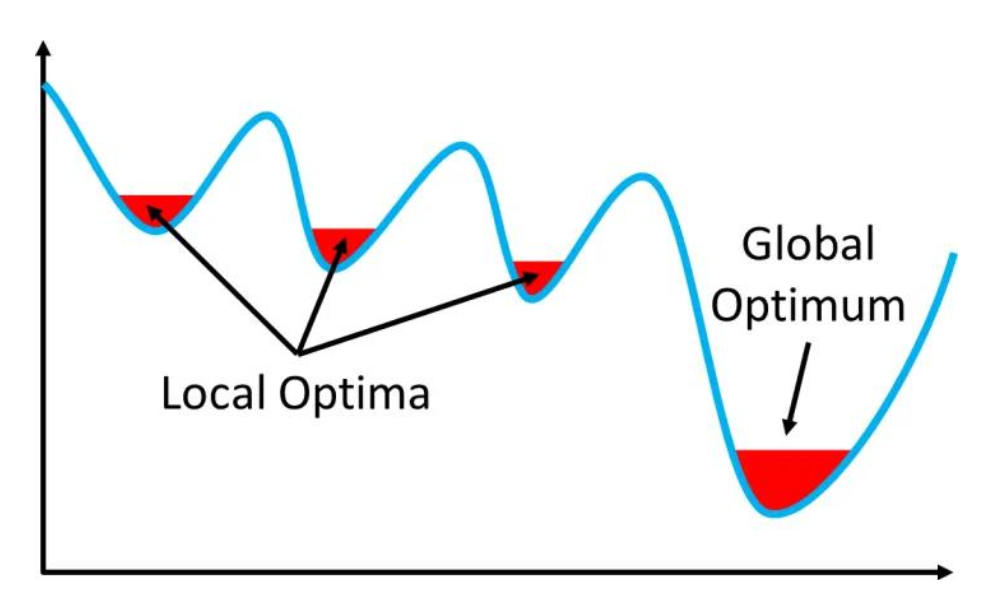
梯度下降法只能找到局部最小值(local minimum)
但对一些函数而言，局部最小就是全局最小

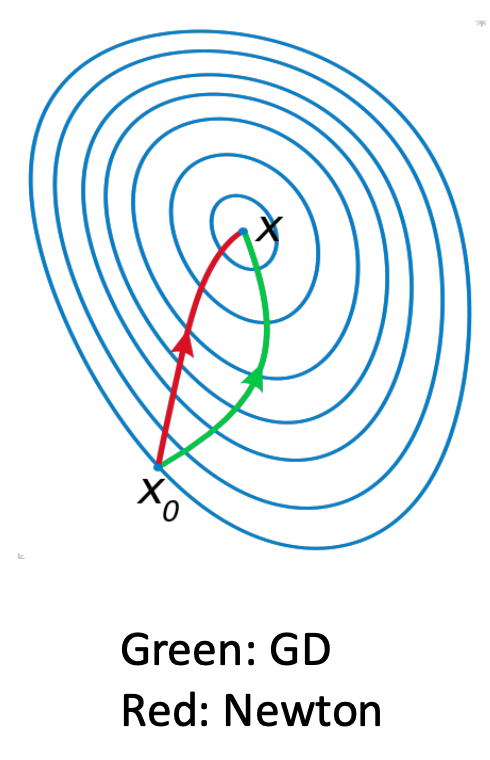
Newton Method⚓︎

第二种方法是牛顿法(Newton method)：

采用二阶泰勒展开

\[ F(x_k + \Delta x) \approx F(x_k) + J_F \Delta x + \dfrac{1}{2} \Delta x^T H_F \Delta x \]
找到最小化 $F(x_k + \Delta x)$ 的 $\Delta x$，满足：

\[ H_F \Delta x + J_F^T = 0 \]
最优方向（牛顿步）为 $\Delta x = -H_F^{-1} J_F^T$
优点：在最小值附近快速收敛
缺点：在黑塞矩阵上要花费大量计算
改进思路：近似计算黑塞矩阵？

Gauss-Newton Method⚓︎

牛顿法的改进方法叫做高斯 - 牛顿法(Gauss-Newton method)。

对求解非线性最小二乘很有用
- 非线性最小二乘
  
  \[ \begin{aligned} \hat{x} & = \arg \min\limits_x F(x) \\ & = \arg \min\limits_x \| R(x) \|_2^2 \end{aligned} \]
  
  其中 $R(x) = \begin{bmatrix}b_1 - f_x(a_1) \\ b_2 - f_x(a_2) \\ \dots \\ b_n - f_x(a_n)\end{bmatrix}$ 是残差向量(residual vector)
  - 我们不展开 $F(x)$，而去展开 $R(x)$
    
    \[ \begin{aligned} \|R(x_k + \Delta x)\|_2^2 & \approx \|R(x_k) + J_R \Delta x\|_2^2 \\ & = \|R(x_k)\|_2^2 + 2R(x_k)^T J_R \Delta x + \Delta x^T J_R^T J_R \Delta x \end{aligned} \]
    
    其中 $J_R$ 是 $R(x)$ 的雅可比矩阵
  - 优化 $\Delta x$，满足
    
    \[ J_R^T J_R \Delta x + J_R^T R(x_k) = 0 \]
因此优化方向 $\Delta x = -(J_R^T J_R)^{-1} J_R^T R(x_k)$
和牛顿法相比
- 牛顿步：$\Delta x = -H_F^{-1} J_F^T$
- 可以看到，高斯 - 牛顿法使用 $J_R^T J_R$ 近似表示 $H_F$
优点：
- 无需计算黑塞矩阵
- 收敛快
缺点：如果 $J_R^T J_R$ 是奇异的，那算法就会不稳定

Levenberg-Marquardt⚓︎

Levenberg-Marquardt 法（以下简称 LM）在高斯 - 牛顿法的基础上引入正则化(regularization)，因此 $$ \Delta x = -(J_R^T J_R \textcolor{red}{+ \lambda I})^{-1} J_R^T R(x_k) $$

其中 $\forall \lambda > 0$，$J_R^T J_R + \lambda I$ 必须是正定矩阵(positive-definite matrix)。

$\lambda$ 的影响：

$\lambda \rightarrow \infty$：梯度下降法，且步长很小
$\lambda \rightarrow 0$：高斯 - 牛顿法

优点：

启动快（$\lambda \uparrow$）
收敛快（$\lambda \downarrow$）
不会退化（$J_R^T J_R + \lambda I$ 必定是正定的）
LM 法 = 梯度下降法 + 高斯 - 牛顿法

Constrained Optimization⚓︎

约束优化(constrained optimization)：目标 (objective) + 约束 (constraints)

不同的方法有不同的约束类型：

凸优化 (convex optimization)

Robust Estimation⚓︎

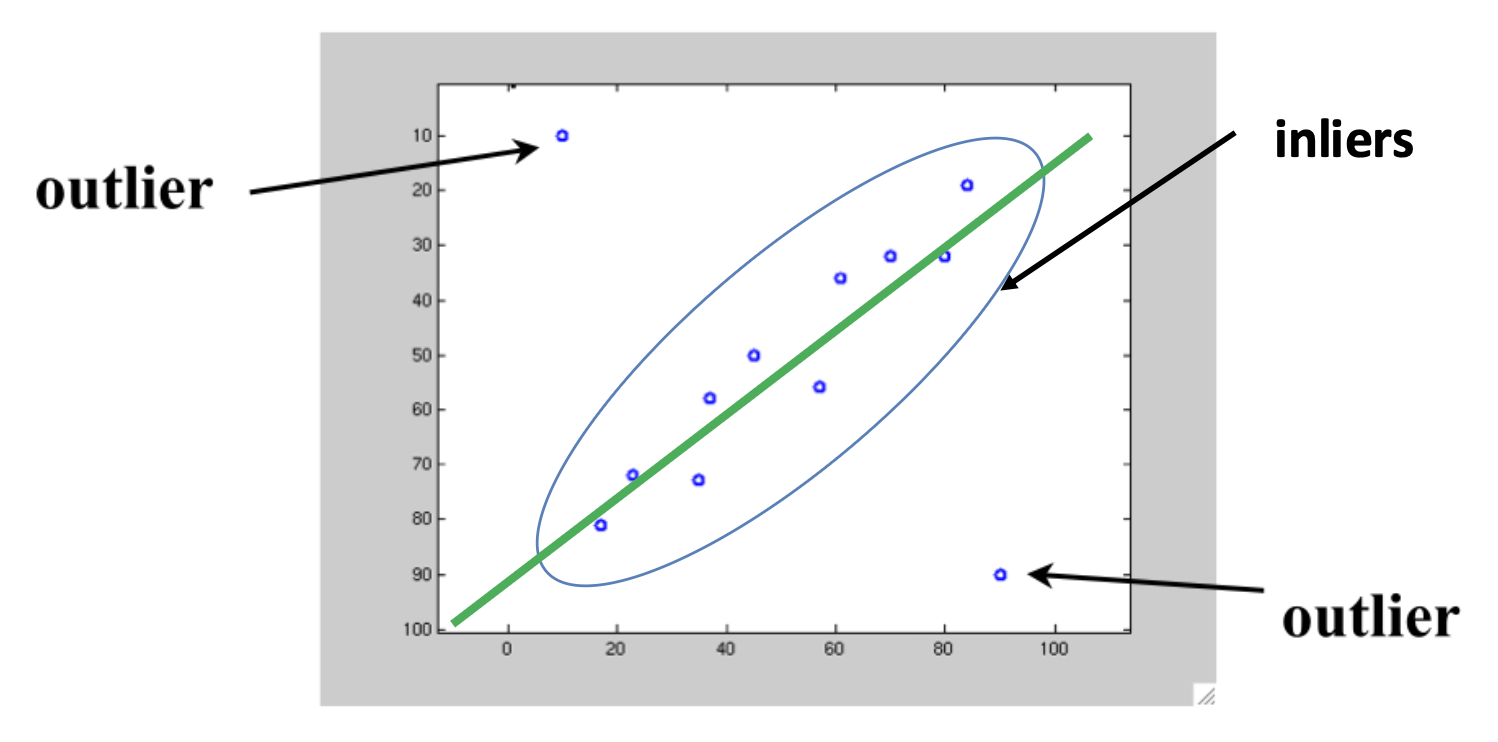
内点(inlier)：遵循模型假设的数据点
异常点(outlier)：和假设有显著差异的数据点

对于以下情况，MSE 失效了：

原因：

MSE 与残差平方成正比
受大量异常点影响

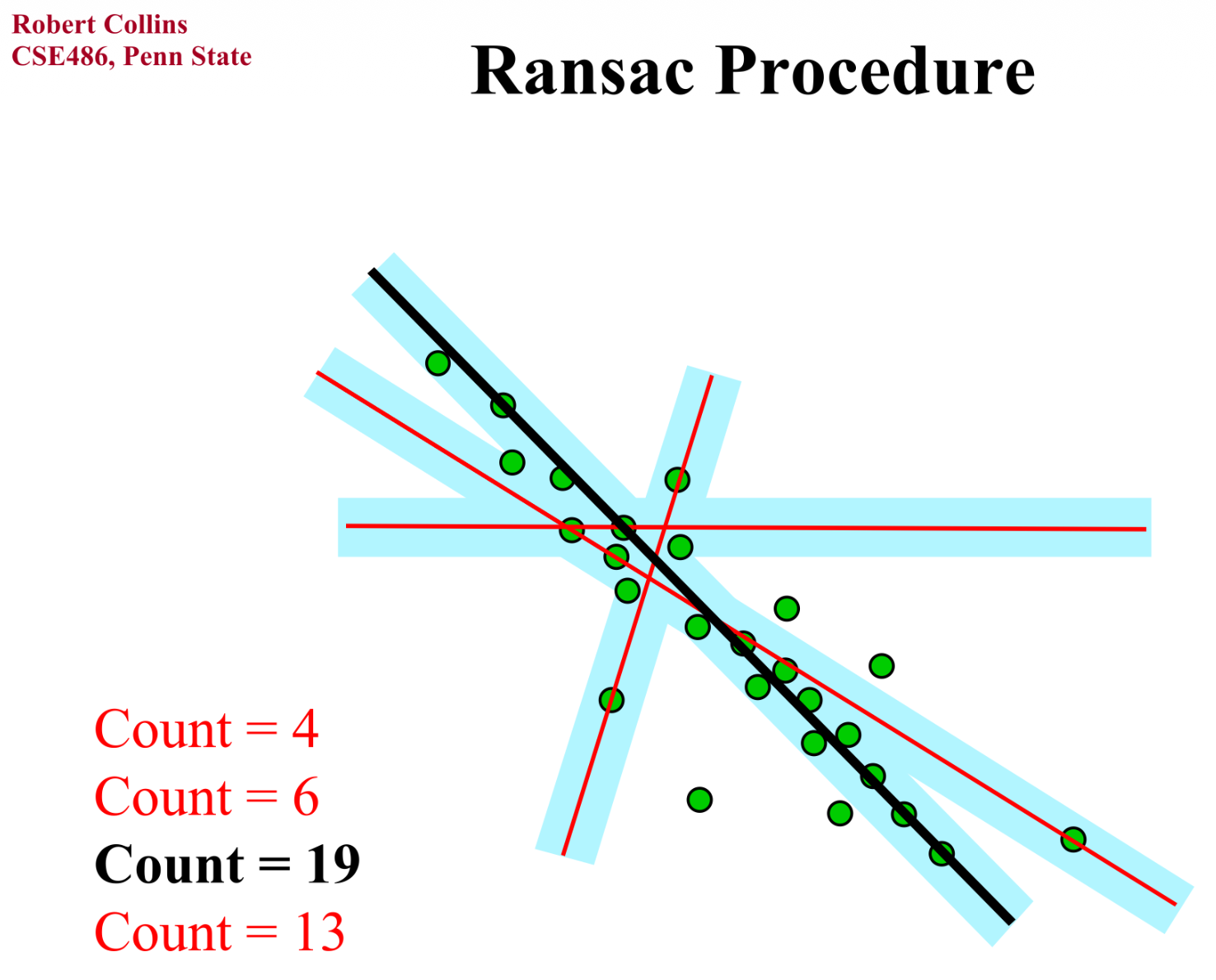
RANSAC⚓︎

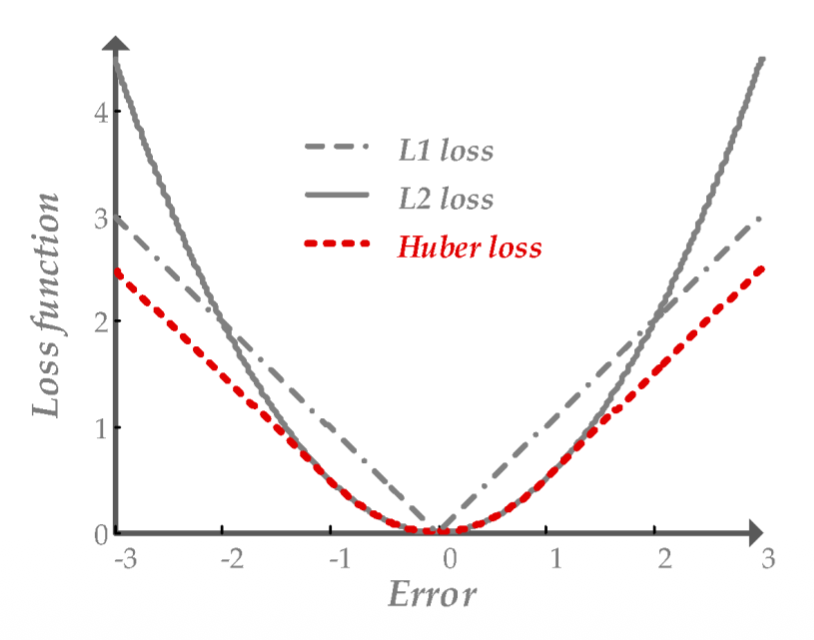
为减小异常点对估计带来的影响，我们需要用别的损失函数来替代 MSE，比如 L1，Huber 等。像这些函数被称为鲁棒函数(robust function)。

其中，最强大的处理异常点的方法是 RANSAC（随机抽样一致 (random sample concensus)），其关键思想为：

内点的分布是相似的，而外点之间的差距很大
使用数据点对进行投票

例子

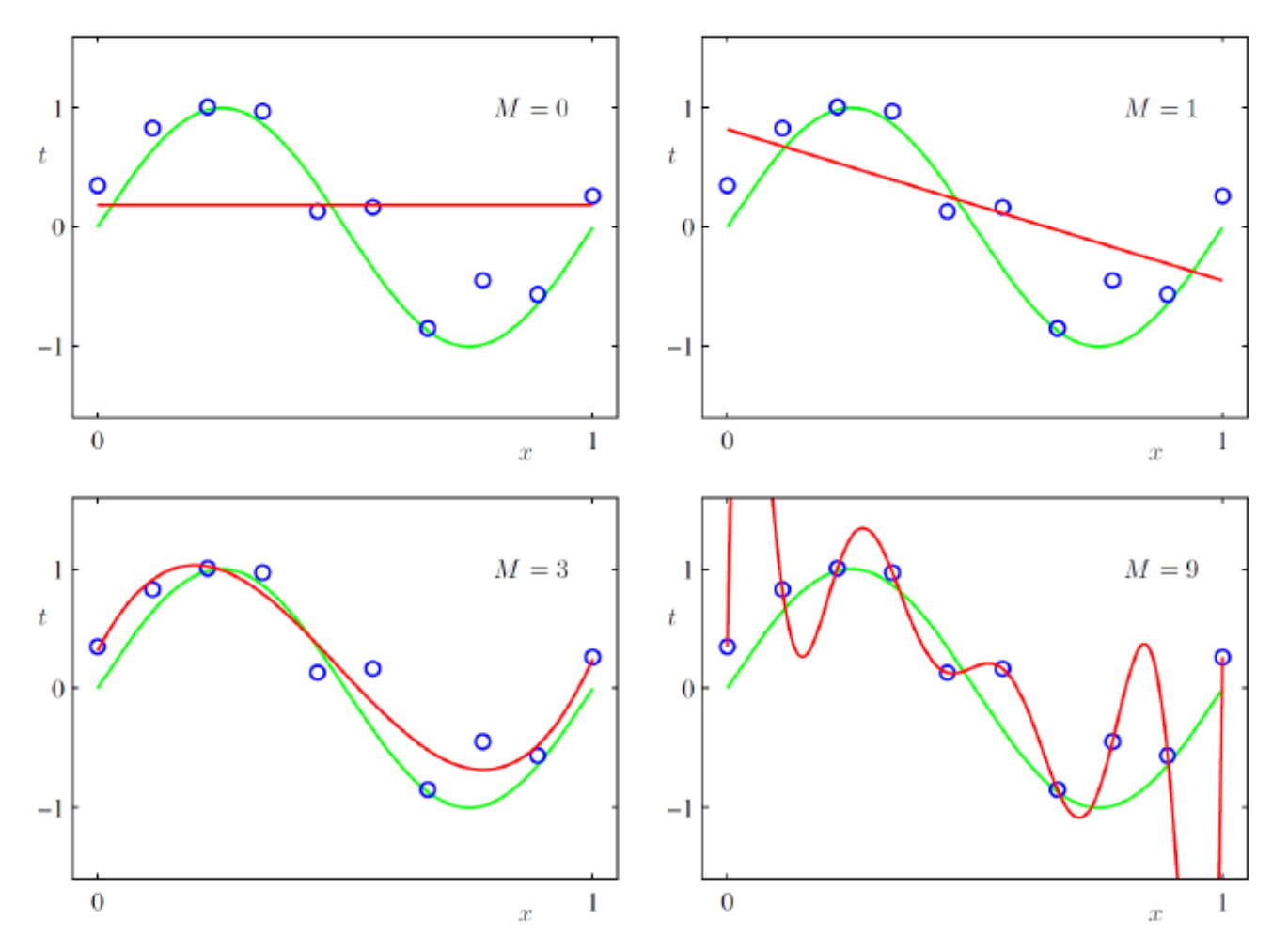
Overfitting and Underfitting⚓︎

不适定问题(ill-posed problem)：解不唯一

比如对于 $\min_x \|Ax - b\|^2$ 方程数少于变量数的时候
可通过利用先验知识增加更多约束来获得唯一解

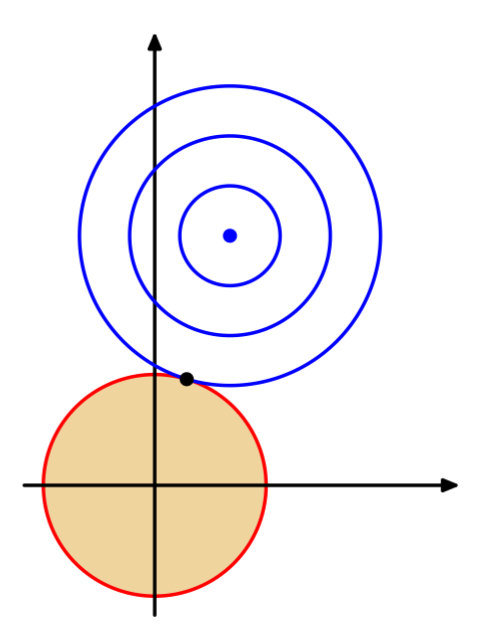
L2 Regularization⚓︎

L2 范数(norm)：$\|x\|_2 = \sum_i x_i^2$
L2 正则化：

\[ \begin{aligned} & \min_x \|Ax - b\|_2^2 \\ & \text{s.t. } \|x\|_2 \le 1 \end{aligned} \]
- 令 $x \rightarrow 0$
- 抑制冗余变量

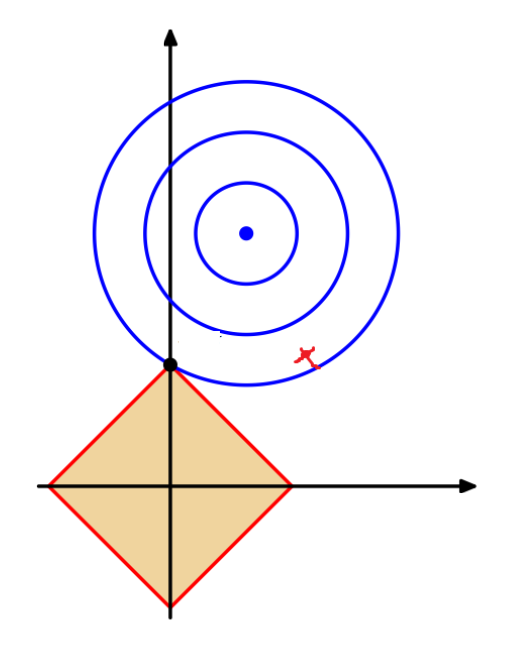
L1 Regularization⚓︎

L1 范数(norm)：$\|x\|_1 = \sum_i x_i$
L2 正则化：

\[ \begin{aligned} & \min_x \|Ax - b\|_2^2 \\ & \text{s.t. } \|x\|_1 \le 1 \end{aligned} \]
- 令 $x$ 稀疏

评论区

如果大家有什么问题或想法，欢迎在下方留言~